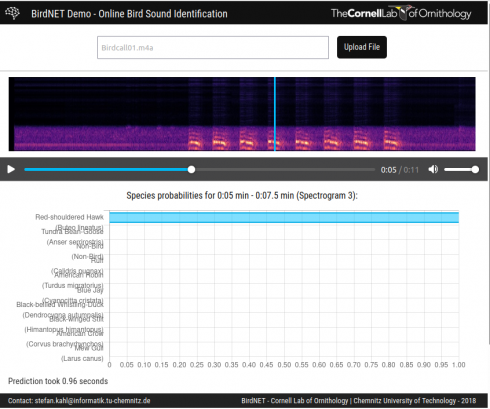
The Cornell Ornithology Lab’s BirdNet lets you upload audio files of bird calls and identifies the birds. I tried it with this file (BirdCall01.m4a) recorded near school, and it identified Red Shouldered Hawks (about 6 seconds in).
Middle and High School … from a Montessori Point of View
The Cornell Ornithology Lab’s BirdNet lets you upload audio files of bird calls and identifies the birds. I tried it with this file (BirdCall01.m4a) recorded near school, and it identified Red Shouldered Hawks (about 6 seconds in).

Video by Tobais Friedrich out of the University of Hawaii. It’s based on a recent paper that suggests that the large fluctuations in climate over the last 120,000 years opened and closed green corridors that allowed multiple pulses of migration out of Africa.
He has some other excellent earth science scientific visualizations.
The reintroduction of wolves to Yellowstone National Park resulted in enormous changes to the ecology: more plants and animals as the wolves reduced the deer population and changed the deers’ behavior. The change in vegetation resulted in stabilization of the rivers, so the wolves changed the geomorphology of the park as well.
I’m teaching a numerical methods class that’s partly an introduction to programming, and partly a survey of numerical solutions to different types of problems students might encounter in the wild. I thought I’d look into doing a session on genetic algorithms, which are an important precursor to things like networks that have been found to be useful in a wide variety of fields including image and character recognition, stock market prediction and medical diagnostics.
The ai-junkie, bare-essentials page on genetic algorithms seemed a reasonable place to start. The site is definitely readable and I was able to put together a code to try to solve its example problem: to figure out what series of four mathematical operations using only single digits (e.g. +5*3/2-7) would give target number (42 in this example).
The procedure is as follows:
And this is the code I came up with:
genetic_algorithm2.py
''' Write a program to combine the sequence of numbers 0123456789 and
the operators */+- to get the target value (42 (as an integer))
'''
'''
Procedure:
1. Randomly generate a few sequences (ns=10) where each sequence is 8
charaters long (ng=8).
2. Check how close the sequence's value is to the target value.
The closer the sequence the higher the weight it will get so use:
w = 1/(value - target)
3. Chose two of the sequences in a way that gives preference to higher
weights.
4. Randomly combine the successful sequences to create new sequences (ns=10)
5. Repeat until target is achieved.
'''
from visual import *
from visual.graph import *
from random import *
import operator
# MODEL PARAMETERS
ns = 100
target_val = 42 #the value the program is trying to achieve
sequence_length = 4 # the number of operators in the sequence
crossover_rate = 0.3
mutation_rate = 0.1
max_itterations = 400
class operation:
def __init__(self, operator = None, number = None, nmin = 0, nmax = 9, type="int"):
if operator == None:
n = randrange(1,5)
if n == 1:
self.operator = "+"
elif n == 2:
self.operator = "-"
elif n == 3:
self.operator = "/"
else:
self.operator = "*"
else:
self.operator = operator
if number == None:
#generate random number from 0-9
self.number = 0
if self.operator == "/":
while self.number == 0:
self.number = randrange(nmin, nmax)
else:
self.number = randrange(nmin, nmax)
else:
self.number = number
self.number = float(self.number)
def calc(self, val=0):
# perform operation given the input value
if self.operator == "+":
val += self.number
elif self.operator == "-":
val -= self.number
elif self.operator == "*":
val *= self.number
elif self.operator == "/":
val /= self.number
return val
class gene:
def __init__(self, n_operations = 5, seq = None):
#seq is a sequence of operations (see class above)
#initalize
self.n_operations = n_operations
#generate sequence
if seq == None:
#print "Generating sequence"
self.seq = []
self.seq.append(operation(operator="+")) # the default operation is + some number
for i in range(n_operations-1):
#generate random number
self.seq.append(operation())
else:
self.seq = seq
self.calc_seq()
#print "Sequence: ", self.seq
def stringify(self):
seq = ""
for i in self.seq:
seq = seq + i.operator + str(i.number)
return seq
def calc_seq(self):
self.val = 0
for i in self.seq:
#print i.calc(self.val)
self.val = i.calc(self.val)
return self.val
def crossover(self, ingene, rate):
# combine this gene with the ingene at the given rate (between 0 and 1)
# of mixing to create two new genes
#print "In 1: ", self.stringify()
#print "In 2: ", ingene.stringify()
new_seq_a = []
new_seq_b = []
for i in range(len(self.seq)):
if (random() < rate): # swap
new_seq_a.append(ingene.seq[i])
new_seq_b.append(self.seq[i])
else:
new_seq_b.append(ingene.seq[i])
new_seq_a.append(self.seq[i])
new_gene_a = gene(seq = new_seq_a)
new_gene_b = gene(seq = new_seq_b)
#print "Out 1:", new_gene_a.stringify()
#print "Out 2:", new_gene_b.stringify()
return (new_gene_a, new_gene_b)
def mutate(self, mutation_rate):
for i in range(1, len(self.seq)):
if random() < mutation_rate:
self.seq[i] = operation()
def weight(target, val):
if val <> None:
#print abs(target - val)
if abs(target - val) <> 0:
w = (1. / abs(target - val))
else:
w = "Bingo"
print "Bingo: target, val = ", target, val
else:
w = 0.
return w
def pick_value(weights):
#given a series of weights randomly pick one of the sequence accounting for
# the values of the weights
# sum all the weights (for normalization)
total = 0
for i in weights:
total += i
# make an array of the normalized cumulative totals of the weights.
cum_wts = []
ctot = 0.0
cum_wts.append(ctot)
for i in range(len(weights)):
ctot += weights[i]/total
cum_wts.append(ctot)
#print cum_wts
# get random number and find where it occurs in array
n = random()
index = randrange(0, len(weights)-1)
for i in range(len(cum_wts)-1):
#print i, cum_wts[i], n, cum_wts[i+1]
if n >= cum_wts[i] and n < cum_wts[i+1]:
index = i
#print "Picked", i
break
return index
def pick_best(weights):
# pick the top two values from the sequences
i1 = -1
i2 = -1
max1 = 0.
max2 = 0.
for i in range(len(weights)):
if weights[i] > max1:
max2 = max1
max1 = weights[i]
i2 = i1
i1 = i
elif weights[i] > max2:
max2 = weights[i]
i2 = i
return (i1, i2)
# Main loop
l_loop = True
loop_num = 0
best_gene = None
##test = gene()
##test.print_seq()
##print test.calc_seq()
# initialize
genes = []
for i in range(ns):
genes.append(gene(n_operations=sequence_length))
#print genes[-1].stringify(), genes[-1].val
f1 = gcurve(color=color.cyan)
while (l_loop and loop_num < max_itterations):
loop_num += 1
if (loop_num%10 == 0):
print "Loop: ", loop_num
# Calculate weights
weights = []
for i in range(ns):
weights.append(weight(target_val, genes[i].val))
# check for hit on target
if weights[-1] == "Bingo":
print "Bingo", genes[i].stringify(), genes[i].val
l_loop = False
best_gene = genes[i]
break
#print weights
if l_loop:
# indicate which was the best fit option (highest weight)
max_w = 0.0
max_i = -1
for i in range(len(weights)):
#print max_w, weights[i]
if weights[i] > max_w:
max_w = weights[i]
max_i = i
best_gene = genes[max_i]
## print "Best operation:", max_i, genes[max_i].stringify(), \
## genes[max_i].val, max_w
f1.plot(pos=(loop_num, best_gene.val))
# Pick parent gene sequences for next generation
# pick first of the genes using weigths for preference
## index = pick_value(weights)
## print "Picked operation: ", index, genes[index].stringify(), \
## genes[index].val, weights[index]
##
## # pick second gene
## index2 = index
## while index2 == index:
## index2 = pick_value(weights)
## print "Picked operation 2:", index2, genes[index2].stringify(), \
## genes[index2].val, weights[index2]
##
(index, index2) = pick_best(weights)
# Crossover: combine genes to get the new population
new_genes = []
for i in range(ns/2):
(a,b) = genes[index].crossover(genes[index2], crossover_rate)
new_genes.append(a)
new_genes.append(b)
# Mutate
for i in new_genes:
i.mutate(mutation_rate)
# update genes array
genes = []
for i in new_genes:
genes.append(i)
print
print "Best Gene:", best_gene.stringify(), best_gene.val
print "Number of iterations:", loop_num
##
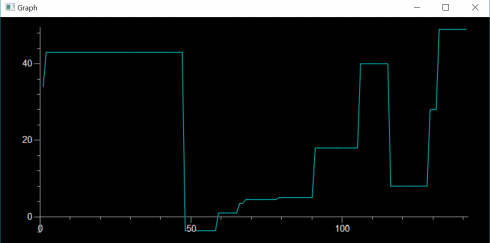
When run, the code usually gets a valid answer, but does not always converge: The figure at the top of this post shows it finding a solution after 142 iterations (the solution it found was: +8.0 +8.0 *3.0 -6.0). The code is rough, but is all I have time for at the moment. However, it should be a reasonable starting point if I should decide to discuss these in class.
A couple new article relevant to our study of Earth History.
Carbon
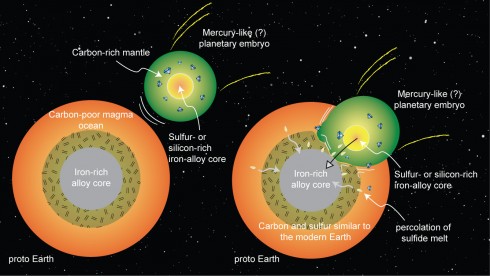
Research on the high pressure and temperature conditions at the Earth’s core suggest that most of the carbon in the early Earth should have either boiled off into space or been trapped by the iron in the core. So where did all the carbon necessary for life come from? They suggest from the collision of an embryonic planet (with lots of carbon in its upper layers) early in the formation of the solar system.
Free Oxygen
It took a few billion years from the evolution of the first photosynthetic cyanobacteria to the time when there was enough oxygen in the atmosphere to support animal life like us. Why did it take so long? NPR interviews scientists investigating purple microbial mats in Lake Huron.
Ed Hawkins posted this extremely useful visualization of month-by-month, global temperature changes since 1850.
What happened:
Detailed article from Mashable: The poisoning of a city
A timeline from Michigan Radio: TIMELINE: Here’s how the Flint water crisis unfolded
An excellent, detailed program from Reveal: Do not drink: The water crisis in Flint, Michigan. The second part in particular is a good summary of the science issues.
A NPR summary from September 29th, 2015: High Lead Levels In Michigan Kids After City Switches Water Source
The Siege of Miami: A detailed report that looks at the increasing frequency of flooding in Miami, because of sea-level-rise. The reporter interviews a number of scientists and engineers who are not terribly optimistic about the long-term (50+ years) future of many Floridian cities because of the melting ice-caps in Greenland and Antarctica.
