I’m teaching a numerical methods class that’s partly an introduction to programming, and partly a survey of numerical solutions to different types of problems students might encounter in the wild. I thought I’d look into doing a session on genetic algorithms, which are an important precursor to things like networks that have been found to be useful in a wide variety of fields including image and character recognition, stock market prediction and medical diagnostics.
The ai-junkie, bare-essentials page on genetic algorithms seemed a reasonable place to start. The site is definitely readable and I was able to put together a code to try to solve its example problem: to figure out what series of four mathematical operations using only single digits (e.g. +5*3/2-7) would give target number (42 in this example).
The procedure is as follows:
- Initialize: Generate several random sets of four operations,
- Test for fitness: Check which ones come closest to the target number,
- Select: Select the two best options (which is not quite what the ai-junkie says to do, but it worked better for me),
- Mate: Combine the two best options semi-randomly (i.e. exchange some percentage of the operations) to produce a new set of operations
- Mutate: swap out some small percentage of the operations randomly,
- Repeat: Go back to the second step (and repeat until you hit the target).
And this is the code I came up with:
genetic_algorithm2.py
''' Write a program to combine the sequence of numbers 0123456789 and
the operators */+- to get the target value (42 (as an integer))
'''
'''
Procedure:
1. Randomly generate a few sequences (ns=10) where each sequence is 8
charaters long (ng=8).
2. Check how close the sequence's value is to the target value.
The closer the sequence the higher the weight it will get so use:
w = 1/(value - target)
3. Chose two of the sequences in a way that gives preference to higher
weights.
4. Randomly combine the successful sequences to create new sequences (ns=10)
5. Repeat until target is achieved.
'''
from visual import *
from visual.graph import *
from random import *
import operator
# MODEL PARAMETERS
ns = 100
target_val = 42 #the value the program is trying to achieve
sequence_length = 4 # the number of operators in the sequence
crossover_rate = 0.3
mutation_rate = 0.1
max_itterations = 400
class operation:
def __init__(self, operator = None, number = None, nmin = 0, nmax = 9, type="int"):
if operator == None:
n = randrange(1,5)
if n == 1:
self.operator = "+"
elif n == 2:
self.operator = "-"
elif n == 3:
self.operator = "/"
else:
self.operator = "*"
else:
self.operator = operator
if number == None:
#generate random number from 0-9
self.number = 0
if self.operator == "/":
while self.number == 0:
self.number = randrange(nmin, nmax)
else:
self.number = randrange(nmin, nmax)
else:
self.number = number
self.number = float(self.number)
def calc(self, val=0):
# perform operation given the input value
if self.operator == "+":
val += self.number
elif self.operator == "-":
val -= self.number
elif self.operator == "*":
val *= self.number
elif self.operator == "/":
val /= self.number
return val
class gene:
def __init__(self, n_operations = 5, seq = None):
#seq is a sequence of operations (see class above)
#initalize
self.n_operations = n_operations
#generate sequence
if seq == None:
#print "Generating sequence"
self.seq = []
self.seq.append(operation(operator="+")) # the default operation is + some number
for i in range(n_operations-1):
#generate random number
self.seq.append(operation())
else:
self.seq = seq
self.calc_seq()
#print "Sequence: ", self.seq
def stringify(self):
seq = ""
for i in self.seq:
seq = seq + i.operator + str(i.number)
return seq
def calc_seq(self):
self.val = 0
for i in self.seq:
#print i.calc(self.val)
self.val = i.calc(self.val)
return self.val
def crossover(self, ingene, rate):
# combine this gene with the ingene at the given rate (between 0 and 1)
# of mixing to create two new genes
#print "In 1: ", self.stringify()
#print "In 2: ", ingene.stringify()
new_seq_a = []
new_seq_b = []
for i in range(len(self.seq)):
if (random() < rate): # swap
new_seq_a.append(ingene.seq[i])
new_seq_b.append(self.seq[i])
else:
new_seq_b.append(ingene.seq[i])
new_seq_a.append(self.seq[i])
new_gene_a = gene(seq = new_seq_a)
new_gene_b = gene(seq = new_seq_b)
#print "Out 1:", new_gene_a.stringify()
#print "Out 2:", new_gene_b.stringify()
return (new_gene_a, new_gene_b)
def mutate(self, mutation_rate):
for i in range(1, len(self.seq)):
if random() < mutation_rate:
self.seq[i] = operation()
def weight(target, val):
if val <> None:
#print abs(target - val)
if abs(target - val) <> 0:
w = (1. / abs(target - val))
else:
w = "Bingo"
print "Bingo: target, val = ", target, val
else:
w = 0.
return w
def pick_value(weights):
#given a series of weights randomly pick one of the sequence accounting for
# the values of the weights
# sum all the weights (for normalization)
total = 0
for i in weights:
total += i
# make an array of the normalized cumulative totals of the weights.
cum_wts = []
ctot = 0.0
cum_wts.append(ctot)
for i in range(len(weights)):
ctot += weights[i]/total
cum_wts.append(ctot)
#print cum_wts
# get random number and find where it occurs in array
n = random()
index = randrange(0, len(weights)-1)
for i in range(len(cum_wts)-1):
#print i, cum_wts[i], n, cum_wts[i+1]
if n >= cum_wts[i] and n < cum_wts[i+1]:
index = i
#print "Picked", i
break
return index
def pick_best(weights):
# pick the top two values from the sequences
i1 = -1
i2 = -1
max1 = 0.
max2 = 0.
for i in range(len(weights)):
if weights[i] > max1:
max2 = max1
max1 = weights[i]
i2 = i1
i1 = i
elif weights[i] > max2:
max2 = weights[i]
i2 = i
return (i1, i2)
# Main loop
l_loop = True
loop_num = 0
best_gene = None
##test = gene()
##test.print_seq()
##print test.calc_seq()
# initialize
genes = []
for i in range(ns):
genes.append(gene(n_operations=sequence_length))
#print genes[-1].stringify(), genes[-1].val
f1 = gcurve(color=color.cyan)
while (l_loop and loop_num < max_itterations):
loop_num += 1
if (loop_num%10 == 0):
print "Loop: ", loop_num
# Calculate weights
weights = []
for i in range(ns):
weights.append(weight(target_val, genes[i].val))
# check for hit on target
if weights[-1] == "Bingo":
print "Bingo", genes[i].stringify(), genes[i].val
l_loop = False
best_gene = genes[i]
break
#print weights
if l_loop:
# indicate which was the best fit option (highest weight)
max_w = 0.0
max_i = -1
for i in range(len(weights)):
#print max_w, weights[i]
if weights[i] > max_w:
max_w = weights[i]
max_i = i
best_gene = genes[max_i]
## print "Best operation:", max_i, genes[max_i].stringify(), \
## genes[max_i].val, max_w
f1.plot(pos=(loop_num, best_gene.val))
# Pick parent gene sequences for next generation
# pick first of the genes using weigths for preference
## index = pick_value(weights)
## print "Picked operation: ", index, genes[index].stringify(), \
## genes[index].val, weights[index]
##
## # pick second gene
## index2 = index
## while index2 == index:
## index2 = pick_value(weights)
## print "Picked operation 2:", index2, genes[index2].stringify(), \
## genes[index2].val, weights[index2]
##
(index, index2) = pick_best(weights)
# Crossover: combine genes to get the new population
new_genes = []
for i in range(ns/2):
(a,b) = genes[index].crossover(genes[index2], crossover_rate)
new_genes.append(a)
new_genes.append(b)
# Mutate
for i in new_genes:
i.mutate(mutation_rate)
# update genes array
genes = []
for i in new_genes:
genes.append(i)
print
print "Best Gene:", best_gene.stringify(), best_gene.val
print "Number of iterations:", loop_num
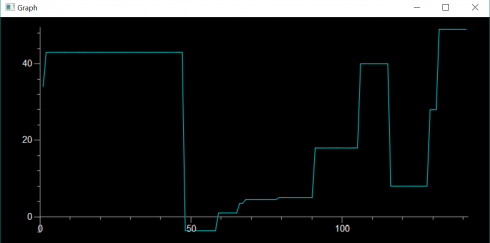
##
When run, the code usually gets a valid answer, but does not always converge: The figure at the top of this post shows it finding a solution after 142 iterations (the solution it found was: +8.0 +8.0 *3.0 -6.0). The code is rough, but is all I have time for at the moment. However, it should be a reasonable starting point if I should decide to discuss these in class.