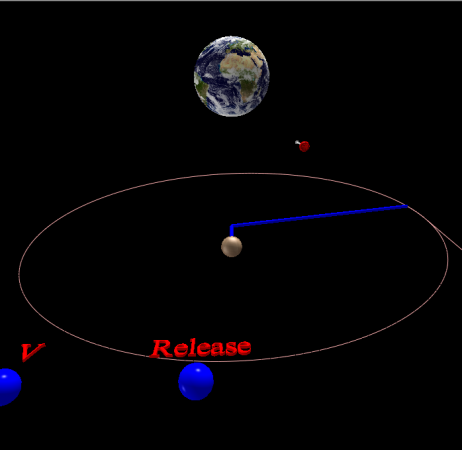
Sitting in a car that’s going around a sharp bend, its easy to feel like there’s a force pushing you against the side of the car. It’s called the centrifugal force, and while it’s real to you as you rotate with the car, if you look at things from the outside (from a frame of reference that’s not rotating) there’s really no force pushing you outward. The only force is the one keeping you in the car; the force of the side of the car on you. This is the centripetal force. Given all the potential for confusion, I created this little VPython model that mimics a sling.
Centripetal Force
In the model, you launch a ball and it goes off in a straight line. That’s inertia. An object will move in a straight line unless there’s some other force acting on it. When the ball hits the string, it catches and the string starts to pull on the ball, taking it away from its straight line trajectory. The force that pulls the ball away from its original straight path is the centripetal force.

Conservation of Angular Momentum
The ball rotating on the sling has an angular momentum (L) that’s equal to the velocity (v) times its mass (m) times its radius (r) away from the center.
L = mvr , angular momentum
Now, angular momentum is conserved, which means that if you shorten the string, reducing the radius, something else must increase to compensate. Since the mass can’t change, the velocity has to, and the ball speeds up.
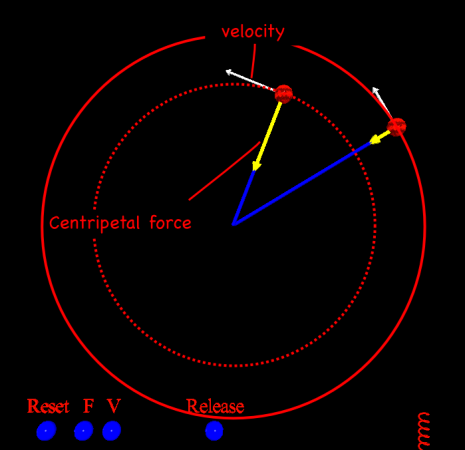
I’ve put in a little ball at the end of the string that you can pull on to shorten the radius.
Tangential Velocity
Once the ball is attached to the string, the centripetal force will keep it moving in a circle. If you release the ball then it will fly off in a straight line in whatever direction it was going when you released it. With no forces acting on the ball, inertia says the ball will move in a straight line.
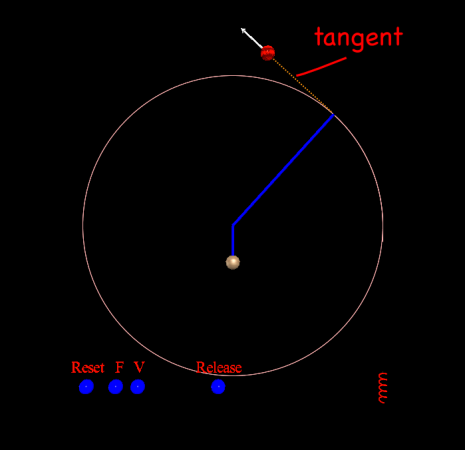
To better illustrate the ball’s motion off a tangent, I put in a target to aim for. It’s off the screen for the normal model view, but if you rotate the scene to look due north you’ll see it.