Inverse Relationships

Inverse relationships pop-up everywhere. They’re pretty common in physics (see Boyle’s Law for example: P ∝ 1/V), but there you sort-of expect them. You don’t quite expect to see them in the number of views of my blog posts, as are shown in the Popular Posts section of the column to the right.

Table 1: Views of the posts on the Montessori Muddle in the previous month as of October 16th, 2012.

Post	Post Rank	Views
Plate Tectonics and the Earthquake in Japan	1	3634
Global Atmospheric Circulation and Biomes	2	1247
Equations of a Parabola: Standard to Vertex Form and Back Again	3	744
Cells, cells, cells	4	721
Salt and Sugar Under the Microscope	5	686
Google Maps: Zooming in to the 5 themes of geography	6	500
Market vs. Socialist Economy: A simulation game	7	247
Human Evolution: A Family Tree	8	263
Osmosis under the microscope	9	219
Geography of data	10	171

You can plot these data to show the relationship.

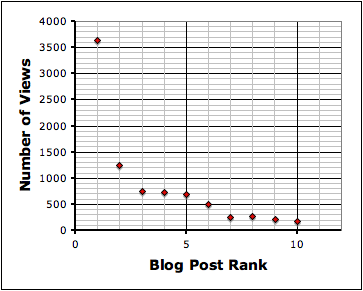
And if you think about it, part of it sort of makes sense that this relationship should be inverse. After all, as you get to lower ranked (less visited) posts, the number of views should asymptotically approach zero.

Questions

So, given this data, can my pre-Calculus students find the equation for the best-fit inverse function? That way I could estimate how many hits my 20th or 100th ranked post gets per month.

Can my Calculus students use the function they come up with to estimate the total number of hits on all of my posts over the last month? Or even the top 20 most popular posts?