
My students and I had a great chance to use the our recent geometry work when we figured out how long it would take to drain the new moat in front of the school.
It’s not really a moat, it’s going to be a flower bed that will soak up some of the runoff that tries to seep into the school’s doors every time a spring or fall thunderstorm sweeps through.
The hole was dug on Thursday evening and filled with rainwater with water, half a meter deep, by Friday morning’s rain. At least we know now that the new beds are in the right place to attract runoff.
But to fill the trenches with gravel, sand and soil, we needed to drain the water. With a small electrical pump it seemed like it would take forever; except that we could do the math.
The pump emptied water through a long hose that runs around the back of the building where the topography is lower. I sent two students with a pitcher and a timer (an iPod Touch actually) to get the flow rate.
They came back with a time of 18.9 seconds to fill 4 liters. I sent them back to take another measurement, and had them average the to numbers to get the more reliable value of 18.65 seconds.
Then one of the students got out the meter-stick and measured the depth of the moat at a few locations. The measurements ranged from 46 cm to about 36 cm and we guesstimated that we could model the moat as having two parts, both sloping. After measuring the length (~6 m) and width (2 m), we went inside to do the math.
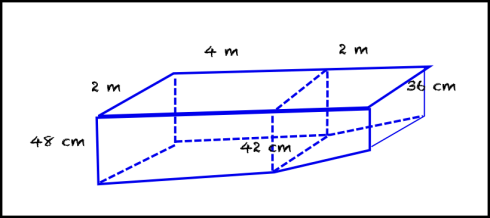
With the help of two of my students who tend to take the advanced math option every cycle, we calculated the volume of water (in cm3) and the flow rate of the pumped water (0.2145 cm3/s). Then we could work out the time it would take to drain the water, which turned out to be a pretty large number of seconds. We converted to minutes and then hours. The final result was about 7 hours, which would mean that the pump would need to run until 10 pm.
And it did.
