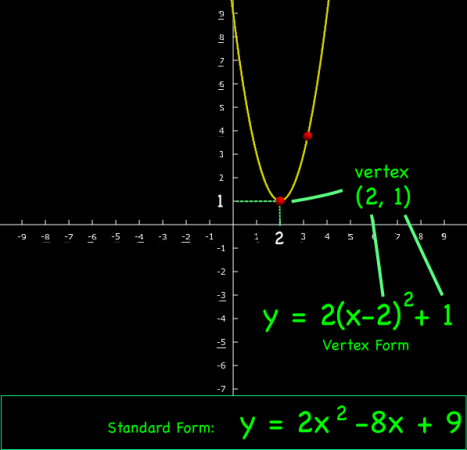
The equation for a parabola is usually written as:

Standard form:
$! y = ax^2 + bx + c$

where a, b and c are constants. This is the form displayed in both the VPython Parabola and Excel parabola programs. However, to make the movement of the curve easier, the VPython program also uses the vertex form of the equation internally:

Vertex Form:
$! y = a(x-h)^2 + k$

where the point (h, k) is the location of the vertex of the parabola. In the example above, h = 1 and k = 2.

To translate between the two forms of the equation, you have to rewrite them. Start by expanding the vertex form:

y = a(x – h)² + k

becomes:

y = a(x – h)(x – h) + k

multiplied out to get:

y = a(x² – 2hx + h²) + k

now distribute the a:

y = ax² – 2ahx + ah² + k

finally, group all the coefficients:

y = (a)x² – (2ah)x + (ah² + k)

This equation has the same form as y = ax² + bx + c if:

Vertex to Standard Form:

a = a
b = -2ah
c = ah²+k

And we can rearrange these equations to go the other way, to find the vertex form from the standard form:

Standard to Vertex Form:

$! a = a$
$! h = \frac{\displaystyle -b}{\displaystyle 2a}$
$! k = c - ah^2 = c - \frac{\displaystyle b^2}{\displaystyle 4a}$

Summary

In sum, you can write the standard equation for a parabola as:

Standard form:

And you can write the equation for the same parabola in vertex form as:

Vertex form:

UPDATES

UPDATE 1: This app will automatically convert from standard to vertex form (or back again).

UPDATE 2: Automatically generate and embed graphs using this parabolic grapher app.