Emission Spectra: How Atoms Emit and Absorb Light

Emission and absorption spectrum of Hydrogen. Image adapted from the one by Wikimedia Commons User:Adrignola.

When a photon of light hits an atom three things can happen: it can bounce off; it can pass through as if nothing had happened; or it be absorbed. Which one happens depends on the energy of the light, and which atom it is hitting. Hydrogen will absorb different energies from helium.

The interesting thing is that each atom will only absorb photons with exactly the right energy. You see, when the light hits the atom, the atom will only absorb it if it can use it to bump an electron up an electron shell.

An oxygen atom with two electrons in the innermost shell and six in the second shell.

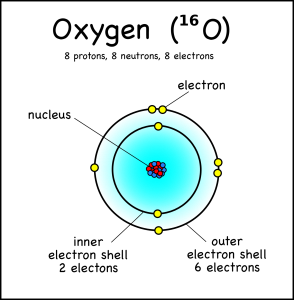
An oxygen atom, for example, has eight electrons, but these fit into two different electron shells. The innermost shell can only hold two electrons, so the other six go into the second shell (which can take a maximum of 8). This is the “ground state” of the atom, because it takes the least amount of energy to keep the electrons in place.

However, if the atom gets hit by just enough energy, one of the electrons can be bumped up into a higher shell. The atom will be “excited” and “want” the electron to drop back down to the lower shell.

And when the electron drops back, it will release the exact same amount of energy that it took to move it up a shell in the first place.

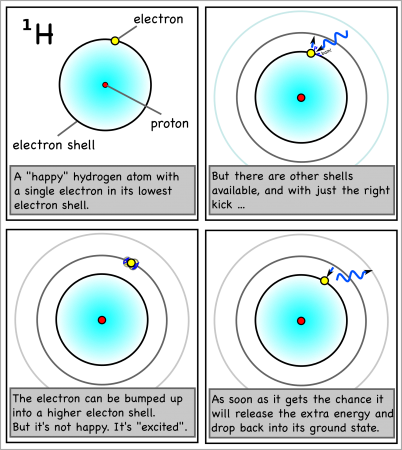
A hydrogen atom's electron is bumped up an energy level/shell by ultraviolet light, but releases that light when the electron drops back down to its original shell.

For hydrogen, the energy to bump up an electron from its first to its second electron shell comes only from light with a wavelength of 1216 x 10-10m (see here for how to calculate). This is in the ultraviolet range, which we can’t see with the naked eye.

However, the energy absorbed and released when the electron moves between the second and fourth shells is 6564 x 10-10m, which is in the visible range. In fact, it’s the red line on the right side of the emission spectrum shown at the top of the page.

The visible part of the emission spectrum of hydrogen and its corresponding electron shell jumps. Note that different colors of light have different energies, and that the blue light is more energetic (and has a shorter wavelength) than red light.

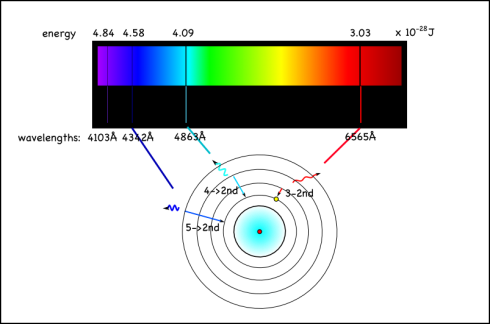
Since this emission signature is unique for each element, looking at the colors of other stars, or the tops of the atmospheres of other planets, is a good way of identifying the elements in them. You can also do flame tests to identify different elements.

Copper.
Lithium.
Sodium.

The University of Oregon has an excellent little Flash application that shows the absorption spectrum of most of the elements in the periodic table (NOTE that the wavelengths they give are in Angstroms (Å) which are 1×10-10m; or tenths of a nanometer (nm)).

Interactive app that shows the absorption spectrum of the elements in the periodic table. From the University of Oregon. Wavelengths are in Angstroms (Å), and 1 Å = 0.1 nm.

Equations

The wavelength of light emitted for the movement of an electron between the electron shells of a hydrogen atom is given by the Rydberg formula:

\frac{1}{\lambda} = R \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right)

where:
\lambda = wavelength of the light in a vacuum
R = Rydberg constant (1.1×107 m-1)
n_1 and n_2 are the electron shell numbers (the innermost shell is 1, the next shell is 2 etc.)

— see an example calculation here.

The amount of energy that corresponds to a particular wavelength of light is given by:

E = \frac{hc}{\lambda}

where:
E = Energy (J),
\lambda = wavelength of the light in a vacuum (m),
h = 6.6×10-34 Js,
c = speed of light in a vacuum (3×108 m/s).

— via Wikipedia.

References

The National Institute of Standards and Technology (NIST) has more extensive emission spectra data.

Leave a Reply