Author: Lensyl Urbano

Flame Tests

Copper burns green.

Elements can be identified from the color of light they give off when they’re ionized: their emission spectra. Ms. Wilson’s chemistry class today set fire to some metal salts to watch them burn.

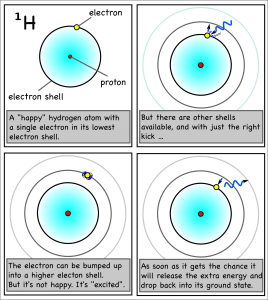
A hydrogen atom's electron is bumped up an energy level/shell by ultraviolet light, but releases that light when the electron drops back down to its original shell.

She placed the salt crystals into petri dishes, submerged them in a shallow layer of alcohol, and ignited the alcohol. As traces of the salts were incorporated into the flames, the metal atoms became “excited” as they absorbed some of the energy from the flame by bumping up their electrons into higher electron shells. Since atoms don’t “like” to be excited, their excited electrons quickly dropped back to their stable, ground state, but, in doing so, released the excess energy as light of the characteristic wavelength.

Table 1: Emission colors of different metals.

Metal Flame
Copper
Strontium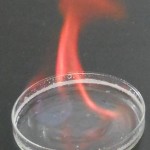
Sodium
Lithium

Mycorrhiza: Symbiosis Between Fungi and Plants

Symbiosis in action (specifically an example of mutualism):

Fungus (white) attached to the roots of a small pine tree (brown). Image via Wikipedia User:Silk666.

The Amanita [mushroom] family also includes some of the best-known tree-partnering fungi on Earth. Many of the mushrooms in this family are mycorrhizae — fungi that coil themselves in and around the roots of trees.

The tree provides them with food it makes topside in return for a vastly improved underground absorptive network. This network, made by the many searching filaments of the fungus, brings much more water and many more minerals to the tree than it would otherwise be able to procure for itself.

— Frazer (2012): Deadly and Delicious Amanitas Can No Longer Decompose on The Artful Amoeba Blog in Scientific American.

Redwood saplings with (right) and without (left) mycorrhizae. Image by Mike Amaranthus, USDA.

In fact:

Some plants are “mycorrhizal-obligate,” meaning that they can’t survive to maturity without their fungal associate. Important mycorrhizal-obligate plants in western North America are sagebrush, bitterbrush, and some native bunchgrasses.

— BLM: Mycorrhizal Fungi

This comes from an interesting article by Jennifer Frazer on Amanita mushrooms, which are so symbiotic with their plant hosts that not only do they not decay them, they actually can’t decay them.

Cave Formation in the Ozarks

Ceiling of Twin Cave.

Rain falls.
Some runs off,
Some seeps into the ground.

Water drips from the tips of limestone straws on the roof of Twins Cave.

It trickles through soil.
Leaching acids, organic,
Out of the leaf litter,

But even without these,
It’s already, every so slightly, corrosive,
From just the carbon dioxide in the air.

Gravity driven,
The seeping water seeks the bedrock,
Where it might find,
In the Ozark Mountains,
Limestone.

Planktonic shell (from Coon Creek which is 30 million years old, compared to the limestone rocks in the Ozarks which are 300 million years old.)

Limestone:
Microscopic shells, of plankton,
Raining down, over millenia,
Compacting into rocks,
In a closing ocean,
As North America and Africa collide,
From the Devonian to the Carboniferous.

Orogenic uplift,
Ocean-floor rocks,
Become mountains,

Appalachians, Ouachitas,
The Ozark Plateau.

The collision of North America and Africa uplifted the limestone rocks from the closing ocean (the Rheic Ocean) to create the Ouachita Mountains and Ozark Plateau. (Figure adapted from iimage by Dr. Ron Blakey - http://jan.ucc.nau.edu/~rcb7).

Limestone dissolves,
In acid water.
Shaping holes; caves in bedrock,
Where we go,
Exploring.

Crawling through the "Brith Canal".

Evolution in Action

A fascinating study of 56,000 generations of bacteria, in 12 different populations, carefully documents how a new ability evolved in one of the populations — the ability to use citrate for food in addition to glucose.

About the key step in the process:

“It wasn’t a typical mutation at all, where just one base-pair, one letter, in the genome is changed,” he said. “Instead, part of the genome was copied so that two chunks of DNA were stitched together in a new way. One chunk encoded a protein to get citrate [for food] into the cell, and the other chunk caused that protein to be expressed.”

— Evolution is as complicated as 1-2-3 from Michigan State University.

That was the second step in a three step process:

The first stage was potentiation, when the E. coli accumulated at least two mutations that set the stage for later events. The second step, actualization, is when the bacteria first began eating citrate, but only just barely nibbling at it. The final stage, refinement, involved mutations that greatly improved the initially weak function. This allowed the citrate eaters to wolf down their new food source and to become dominant in the population.

Note

I’ve been discussing different genres of scientific writing with my middle school class, so it’s interesting to point out that the article this post refers to is just a press release about the actual research paper. These are two very distinct types of scientific writing.

Curve Matching: Radioactive Decay and the Distance Between the Earth and the Sun

According to theory, radioactive elements will always at a constant rate, with a little variability due to randomness. What you should not expect to find is that the rate of decay changes with the distance of the Earth from the Sun.

The rate of radioactive decay of Chlorine-36 (blue x's) seems to be related to the distance between the Earth and the Sun (red line). (Image from Dekant, 2012).

In pre-Calculus, we’re figuring out how to match curves to data. The scientists in this study do something similar, trying to see what types of sinusoidal curves will match the data, then seeing what natural phenomena have the same period (the time it takes for one cycle).

Human Microbiome Project: Figuring out who our Microscopic Symbiotes are, and what they do

Although we are, by number at least, 90% bacteria, only recently have scientists with the Human Microbiome Project have just begun figuring out who those bugs are.

[The] trillions of microbes that make their homes in and on us do an excellent job keeping us healthy (crowding out harmful microbes) and sated (breaking down a lot of the food we ingest).

Now that disturbances in this rich microbiome community have been linked to weight gain, inflammatory bowel disease, vaginal infections and risk for infection with harmful microbes (such as methicillin-resistant Staphylococcus aureus, or MRSA), the importance of understanding what makes up a “healthy” microbiome has become even more apparent.

— Harmon (2012): Body Count: Taking Stock of All the Bugs That Call Humans Home in Scientific American.

Carbide Cannon

Ms. Wilson’s chemistry class is looking at basic chemical reactions, and today they got to fire an acetylene cannon. When calcium carbide (CaC2) reacts with water (H2O) they produce acetylene (C2H2), which is quite explosive.

CaC2 + 2 H2O → C2H2 + Ca(OH)2

Acetylene is so flammable, because its carbons are held together by a triple bond: when the triple bond breaks it releases a lot of energy (about 839 kJ per mole).

Table 1: Bond strengths of simple hydrocarbons with carbon to carbon bonds

Name Chemical Formula Diagram Carbon to Carbon Bond Strength (kJ/mol)
Acetylene C2H2 839
Ethene C2H4 611
Ethane C2H6 347

The explosion is a result of the combustion of the acetylene:

2C2H2 + 5O2 –> 2H2O + 4CO2

And this whole process — carbide plus water to give acetylene, which is then burned — was used by miners in the early 20th century to make headlamps (among other types of lamps).

A carbide lamp (image via Wikipedia).

The cannon itself is a simple device, made of a 50cm tube of 2-3 inch diameter PVC (sorry about the mixed units), with a screw cap at one end. The carbide grains (about 0.5 g) are placed on the inside of the cap, which is then screwed on to the bottom of the tube. A few drops of water are then added through a small hole in the PVC using a plastic dropper — you can listen for the sizzling to tell if the carbide decomposition reaction is happening. Finally a flame is applied to the same hole as the water. The sock, by the way, is just lightly tucked in near the top of the PVC tube, about 5 cm in.

The explosion was loud, and Ms. Wilson’s sock traveled about 10 meters. It was suitably impressive. I think the student who was the most impressed was the one who had weighed out the calcium carbide, becaues 0.5 grams is really only four or five grains.

Ms. Wilson demonstrates the carbide sock cannon.