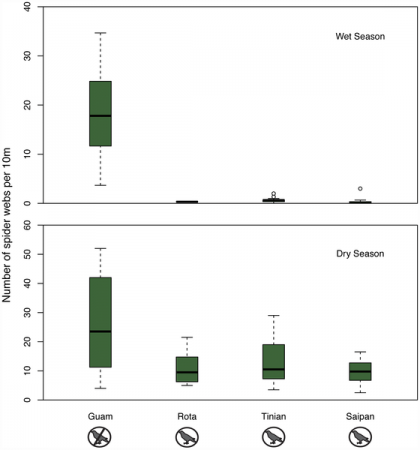
Perhaps the key reason for the profound influence of Darwin’s “On the Origin of Species” is that it’s such a well written and well reasoned argument based on years of study. It is a wonderful example of how science should be done, and how it should be presented. In the past I’ve had my middle schoolers try to translate sections of Darwin’s writing into plainer, more modern English, with some very good results. They pick up a lot of vocabulary, and are introduced to longer, more complex sentences that are, however, clearly written.

The text of “On the Origin of Species” is available for free from the Gutenberg library. Images of the original document can be found (also for free) at the UK website, Darwin Online (which also includes the Darwin’s annotated copy). Darwin Online also hosts lot of Darwin’s other works, as well as notes of the other scientists on The Beagle, among which is included some wonderful scientific diagrams.
This year, I’m going to have the middle schoolers read the introduction, while the honors environmental science students will read selected chapters and present to the class — this will be their off-block assignment.