Exponential Cell Growth

The video shows 300 seconds of purely exponential growth (uninhibited), captured from the exponential growth VAMP scenario. Like the exponential growth function itself, the video starts off slowly then gets a lot more exciting (for a given value of exciting).

The modeled growth is based on the exponential growth function:

$N = N_0 e^{rt}$ (1)

where:

N = number of cells (or concentration of biomass);
N₀ = the starting number of cells;
r = the rate constant, which determines how fast growth occurs; and
t = time.

Finding the Rate Constant/Doubling Time (r)

You can enter either the rate constant (r) or the doubling time of the particular organism into the model. Determining the doubling time from the exponential growth equation is a nice exercise for pre-calculus students.

Let’s call the doubling time, t_d. When the organism doubles from it’s initial concentration the growth equation becomes:

$2N_0 = N_0 e^{r t_d}$

divide through by N₀:

$2 = e^{r t_d}$

take the natural logs of both sides:

$\ln 2 = \ln (e^{r t_d})$

bring the exponent down (that’s one of the rules of logarithms);

$\ln 2 = r t_d \ln (e)$

remember that ln(e) = 1:

$\ln 2 = r t_d$

and solve for the doubling time:

$\frac{\ln 2}{r} = t_d$

Decay

A nice follow up would be to solve for the half life given the exponential decay function, which differs from the exponential growth function only by the negative in the exponent:

$N = N_0 e^{-rt}$

The UCSD math website has more details about Exponential Growth and Decay.

Finding the Growth Rate

A useful calculus assignment would be to determine the growth rate at any point in time, because that’s what the model actually uses to calculate the growth in cells from timestep to timestep.

The growth rate would be the change in the number of cells with time:

$\frac{dN}{dt}$

starting with the exponential growth equation:

$N = N_0 e^{rt}$

since we have a natural exponent term, we’ll use the rule for differentiating natural exponents:

$\frac{d}{dx}(e^u) = e^u \frac{du}{dx}$

So to make this work we’ll have to define:

$u = rt$

which can be differentiated to give:

$\frac{du}{dt} = r$

and since N₀ is a constant:

$N = N_0 e^{u}$

$\frac{dN}{dt} = N_0 e^{u} \frac{du}{dt}$

substituting in for u and du/dt gives:

$\frac{dN}{dt} = N_0 e^{rt} (r)$

rearranging (to make it look prettier (and clearer)):

$\frac{dN}{dt} = N_0 r e^{rt}$ (2)

Numerical Methods: Euler’s method

With this formula, the model could use linear approximations — like in Euler’s method — to simulate the growth of the biomass.

First we can discretize the differential so that the change in N and the change in time (t$) take on discrete values:
$\frac{dN}{dt} = \frac{\Delta N}{\Delta t}$

Now the change in N is the difference between the current value N^t and the new value N^t+1:

Now using this in our differentiated equation (Eq. 2) gives:

$\frac{N^{t+1}-N^t}{\Delta t} = N_0 r e^{r\Delta t}$

Which we can solve for the new biomass (N^^t+1):

$N^{t+1}-N^t = N_0 r e^{r\Delta t} \Delta t$

to get:
$N^{t+1} = N_0 r e^{r\Delta t} \Delta t + N^t$

This linear approximation, however, does introduce some error.

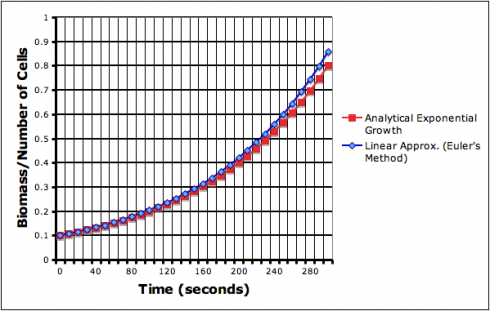
The approximated exponential growth curve (blue line) deviates from the analytical equation. The deviation compounds itself, getting worse exponentially, as time goes on.

Excel file for graphed data: exponential_growth.xls

VAMP

This is the first, basic but useful product of my summer work on the IMPS website, which is centered on the VAMP biochemical model. The VAMP model is, as of this moment, still in it’s alpha stage of development — it’s not terribly user-friendly and is fairly limited in scope — but is improving rapidly.

Epigenetics: How our Environment Affects what our Genes Do.

The middle-school introduction to genetics tends to start with Mendel‘s pea experiments and end with Punnet Squares. The focus is on dominant and recessive genes and what’s expressed given various combinations.

However, the way genes behave are not quite that simple. Tim Spector’s new book, Identically Different, goes into the ways that people’s behavior and environment — the things they eat; the chemicals that surround them — affect the way their genes behave. Even identical twins can be profoundly different depending on things that happen in the womb.

Perhaps the most intriguingly argument is that the behavior of grandparents can affect their grandchildren. In the post World War II period in Britain food was scarce, and some people tended to episodes of starvation alternating with binge eating. Spector links this to an increase in the obesity of their grandkids.

The idea that your behavior can affect the expression of your kids’ genes is more akin to Lamark’s view of evolution than Darwin’s.

↬ The Dish ↬ BrianAppleyard,com.

DarwinTunes: Watching Music Evolve

Take randomly generated sound waves (using sine curves for example), mix them together to get beats, and then let people decide which ones sound best. Let the best ones mate — add in small mutations — and wait a few thousand generations for the sound patterns to evolve into music.

That’s what DarwinTunes does, and they let you participate in the artificial selection process (artificial as opposed to natural selection).

The details are included in their article: Evolution of music by public choice by MacCallum et al. (2012).

Butterfly on the Bench

speyeria-5008 — Great Spangled Fritillary (*Speyeria cybele*). View of the underside of its wings (ventral view).

This little guy seemed to like hanging out on the bench near the back door. I believe it’s a Great Spangled Fritillary (Speyeria cybele).

speyeria-5005 — Dorsal (top down) view of a Great Spangled Fritillary (*Speyeria cybele*).

speyeria-5010 — Great Spangled Fritillary (*Speyeria cybele*).

speyeria-5015 — Great Spangled Fritillary (*Speyeria cybele*).

Spittlebugs

foam-bug-1269 — 40x magnification of the head of the spittlebug nymph.

On the wildgrass-covered slope next to school, you can see a lot of these little foamy things, that look like spit, on the stalks of the tall grasses and herbs.

spit-bugs-4906 — Spittlebug "spit" is mostly made of a froth of the plant's sap.

One of my students collected some to look at under the microscope. We thought it might be the collection of eggs of some creature. It turned out that, at the center of the foam, was what looked like an immature insect. A quick google search for “spit bugs” turned up froghoppers, whose nymphs create the spit to protect them from the environment (heat, cold) and hide themselves from predators.

They suck the sap of the plants they’re on, and can be agricultural pests.

foam-bug-1264 — Spittlebug nymphs on a slide.

Crayfish in the Creek

crayfish-1184 — Crayfish camouflaged against the rocks in the creek.

One of my favorite things about the Fulton School campus is the little creek that runs along the boundary. It’s small, dynamic, and teeming with life.

The crayfish are out in force at the moment. Some of the high-schoolers collected one last fall and it survived the winter in our fish tank (also populated with fish from the creek).

They are quite fascinating to observe; wandering around the sandy bed as if they own the place; aggressive with their pincers occasionally; but then darting backward amazingly fast if they feel threatened.

The one in our tank has just molted a second time, so now we have two almost perfect exoskeletons sitting around the science lab.

crayfish-1233 — Crayfish exoskeleton. From pincers to tail the skeleton is approximately 10cm long.

Harvesting and Processing Chickens

We successfully harvested and processed three chickens during last week’s interim. It was my first time going through the entire process, but fortunately we had a very experienced guide in Dr. Samsone who also happens to be a vet.

The interim focused on where food comes from (students also saw the documentary “King Corn”), and the cleaning of the chickens was tied into our Biology students’ study of anatomy (I’d done fish and squid before). Unfortunately, I was unable to find someone who knew how to read the entrails so we could tie the process into history and language arts as well.

chicken-1085 — Student holds a kidney. A heart is in the background.

When we were done with the processing and analysis, Mr. Elder cooked the chickens on our brand new grill (which worked quite well he says). The chickens were free-range (donated by Ms. Eisenberger), but a little on the old side, at about 7 months old; the chickens you buy at the grocery are somewhere around 2 months old.

Dr. Samsone recommended that next time we raise the chickens ourselves from chicks, which I’d love to try, but I suspect would run into some serious resistance from the students. We’d only had the chickens we harvested for five minutes before they’d all been given names. Raising chickens from chicks would bring a whole new level of anthropomorphizing.

chicken-grill-4826 — Chicken on the grill. The culmination of the interim.

References

Being new to the chickens, I spent a bit of time researching how it is done.

Ken Bolte, from the Franklin County Extension of the University of Missouri, recommended the University of Minnesota’s Extension site on Home Processing of Poultry (the page on evisceration provided an excellent guide), as well as Oklahoma State’s much briefer guide (pdf).

Dr. Samsone recommended the series of videos from the Featherman Equipment Company. Videos are particularly useful for novices like myself.

Herrick Kimball’s excellent How to Butcher a Chicken is also a great reference.

Radish Leaf Pesto

In addition to eating the bulbs of the radishes, the leaves are also edible. I heartily endorse Clotilde Dusoulier’s Radish Leaf Pesto. The slight spiciness of the leaves gives it a delightful frisson.

Pesto recipes are pretty flexible. I added some fresh cilantro from the garden, some frozen basil leaves, used ground almonds for the nut component, a bit of Manchego for the cheese, and doubled the garlic. I also added a little white wine to reduce the viscosity. I quite liked the end result — we had it on pasta — even if some others though it was a little too adventurous.