A wonderful and facinating interpretation of what pi sounds like if you translate the first 33 digits into sounds.
Category: Mathematics
The Middle School Bank and Trust: A Personal Finance Simulation
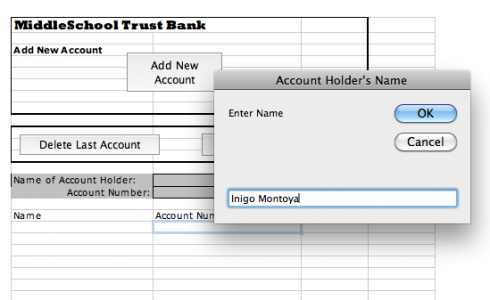
To get students a little more familiar with personal finance, we’re doing a little bank account simulation, and I created a little Excel program to make things a little easier.
It’s really created for the class where students can come up to the bank individually, and the banker/teacher can enter their name and print out their checks as they open their account.
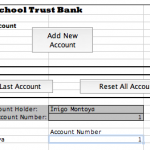
The front sheet of the spreadsheet (called the “Bank Account” sheet) has three buttons. The first, the “Add New Account” button, asks you to enter the student’s name and it assigns the student an account number, which is used on all the checks and deposit slips. The other two buttons let you delete the last account you entered, and reset the entire spreadsheet, respectively.

Once you’ve created an account the spreadsheet updates the “Checks and Deposit Slips” sheet with the student’s name and account number. If you flip to that sheet you can print out eight checks and five deposit slips, which should be enough to get you through the simulation. The checks are numbered and have the student’s account number on them.
There are two other sheets. One is the “Checkbook Register”, which is generic and each student should get one, and the other is called “Customer Balances”. The latter is set up so you (the teacher) can enter all the deposits and withdrawals the students make, and keep track of it all on the same page.
Yes, it’s a bit of overkill, but I though that, since I was going through the effort, I should probably do a reasonable job. Besides, it gave me a chance to do a little Visual Basic programming to keep my hand in. While I teach programming using VPython (see this for example, but I’ll have to do a post about that sometime) you can do some very interesting things in Excel.
Note: I’ve updated the Excel file.
Kilobucks and capitalism
Well, it’s really kilobucks and economic systems, but that does not have the same rhythm for a title. We’re reprising the market versus socialist economies simulation game, my student came up with last year for his IRP.
I though I’d also include a little lesson on the metric system as a subtext. Hence the creation of the kilobuck. I’ll also talk about the centidollar, decidollar, decadollar and hectadollar.

Exercise on Wealth Distribution
Using the actual U.S. wealth distribution data from Norton and Arieli (2011; pdf), I created a little addendum to our exercise on the distribution of wealth.
I started with the definition of wealth. Students tend to think you’re referring to annual income, so I gave the example of someone who does not have a job but owns a house; they have no income but some wealth in the value of the house. Alternately, someone who has $2 million in the bank, but owes $4 million, actually has negative wealth.
Then I drew a little stick figure diagram to represent the population of the United States. With ten figures, paired up, that gives five parts, aka quintiles.
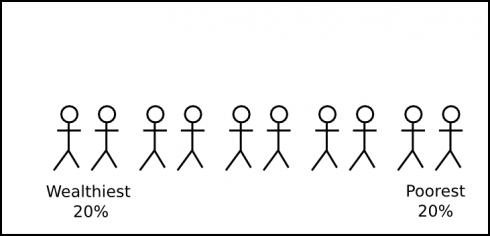
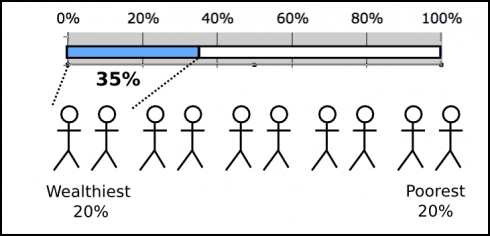
Students were then presented with an empty bar graph and asked, “How much of the U.S.’s wealth is owned by the wealthiest 20% of the population?” Instead of asking in percentages (as are shown in the graph), I asked them to assume that the total wealth in the U.S. is $100 trillion.
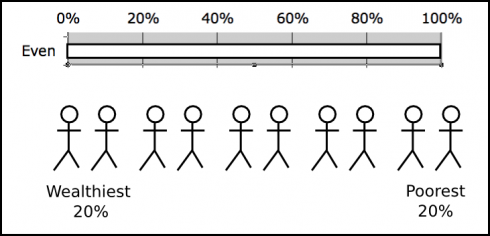
The first suggestion was $35 trillion, which is shown below. Others offered different amounts, ranging up to $50 trillion. Someone even suggested $15 trillion, which is not possible, since that would mean that the wealthiest 20% have less than 20% of the total wealth of the country.
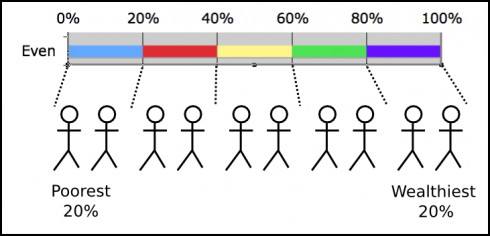
Once they got the idea, I showed them what the graph would look like in an idealized socialist country, where everyone had the same wealth.
Finally, I asked my students to fill in what they believed to be the actual case for the U.S. for all five quintiles. The results had to add up to $100 trillion. They gave me their numbers individually before we broke up our meeting, and I entered it in the U.S. distribution of wealth spreadsheet to produce a graph.
After lunch, I showed them the results.
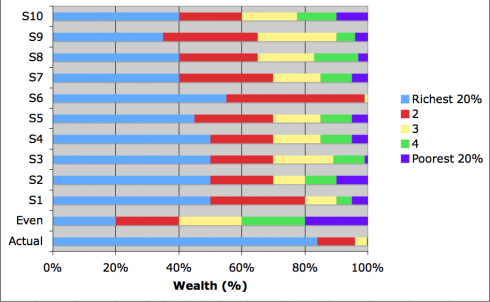
For dramatic effect, I hid the last two bars at first. We talked over their numbers, then I showed them the equal distribution case (which they’d seen before), and finally the actual distribution.
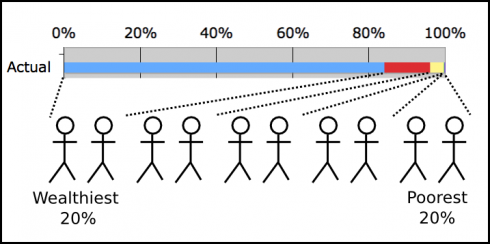
The response was salutary; a moment of surprised silence and then whispers. What then followed was a nice, short discussion. I pointed out the pie charts showing the U.S. versus an equal distribution, versus Sweden and asked what they would do, if they were an autocratic monarch, or if they were the president to make the U.S.’s distribution more equal.
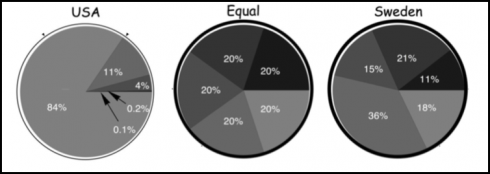
We talked about the government just taking private property, like the communists did. Then we talked about progressive taxation. We ended by talking about the estate tax, and meritocracy, which we’d touched on in the morning.
I thought the exercise worked very well. Not only did we get into an interesting economic issue, but got some practice with math and interpreting graphs too.
Distribution of Wealth
One of our economics assignments this cycle asks students to divvy up $200,000 among a group of ten people. One is a divorced mom, another a playboy, a third a bank manager, you get the gist. The purpose is to compare what students think it should be, to what a socialist might believe, to students’ estimation of reality. I’m really curious to see what they come up with.
Michael Norton and Dan Ariely have some actual data on the wealth distribution in the United States that might really challenge some assumptions (Norton and Ariely, 2011 pdf). They asked survey respondents what percentage of wealth they thought was owned by the poorest 20% of U.S. citizens, the next 20% and so on. They also asked what kind of wealth distribution people though would be ideal. Finally, they compared what people thought to what was actually there.
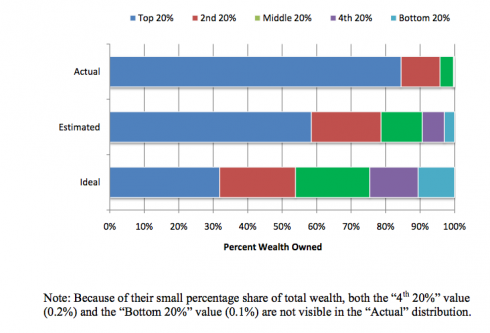
People, apparently, really underestimate the income inequality in the U.S..
A second part of the same study gave people pie charts of wealth distribution in different societies and asked them to pick out which one they would prefer to live in if they were dropped at random into one of these societies. They compared the more socialist-like Sweden, to the U.S., and to a perfectly even distribution. People greatly preferred societies with a more equal sharing of wealth.

I think I’m going to have to modify this assignment to use these graphs. I’ll also have to use their definition of wealth:
Wealth, also known as net worth, is defined as the total value of everything someone owns minus any debt that he or she owes. A person’s net worth includes his or her bank account savings plus the value of other things such as property, stocks, bonds, art, collections, etc., minus the value of things like loans and mortgages.
–Norton and Arieli (2011): Building a Better America – One Wealth Quintile at a Time in Perspectives on Psychological Science
Beating probability
Since we just finished doing a bit of probabilities in math, here’s an article about how one guy figured out how to beat the lottery.
The first lottery Mohan Srivastava decoded was a tic-tac-toe game run by the Ontario Lottery in 2003. He was able to identify winning tickets with 90 percent accuracy.
–Lehrer (2010) in Cracking the Scratch Lottery Code
However, he decided not to just try to get rich of what he’d discovered. It’s an example of using the power of math for good:
“People often assume that I must be some extremely moral person because I didn’t take advantage of the lottery,” [Srivastava] says. “I can assure you that that’s not the case. I’d simply done the math and concluded that beating the game wasn’t worth my time.”
As a side note, my philosophy about the lottery is that it’s basically a tax on the poor:
[H]igh-frequency players tend to be poor and uneducated, which is why critics refer to lotteries as a regressive tax. (In a 2006 survey, 30 percent of people without a high school degree said that playing the lottery was a wealth-building strategy.)
–Lehrer (2010): Cracking the Scratch Lottery Code
Graphing discussion threads

Swings to the right are arguments for keeping the article, swings to the left are arguments to delete them. Moritz Stefaner and others’ website have created this wonderful graphic of Wikipedia’s discussion threads. They have lots more details and discussions on their website.
The Chrysalids, Godwined
As an online discussion grows longer, the probability of a comparison involving Nazis or Hitler approaches 1.
— Mike Godwin, 1989.
Our daily discussions of The Chrysalids have gone on long enough that Hitler came up. I can’t remember the details, but somehow, it occurred to one of my students that, since we don’t know exactly when the story is set, and given the outstanding question, “Did they ever find Hitler’s body?” what if Hitler turned up in the book.
Sigh.
Quite coincidentally, I ran into this article today, about Hitler’s last bodyguard. Apparently, he’s getting too old to answer all his fan mail. Tennessee gets a mention.
Sigh.
On a final note, the above quote about Godwin’s Law is a nice one to use in a cycle where we’re talking about probability.
Cheers.