Tag: exponential growth

Exponential Growth of Cells

Today I grew, and then killed off, a bunch of bacteria using the VAMP exponential growth model to talk about exponential and logarithmic functions in pre-Calculus. I also took the opportunity to use an exponential decay model to talk about the development of drug resistance in bacteria.

Two cells are reproducing (yellow) during a run of the exponential growth model.

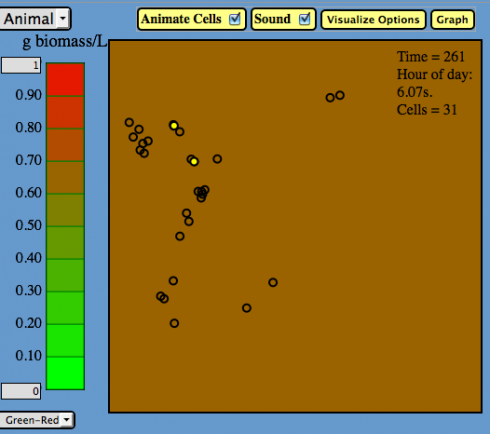
Students had already worked on, and presented to each other, a few bacterial growth problems but the sound and the animation helped give a better conceptual understanding of what was going on.

After watching and listening to the simulation I asked, “What happens to the doubling time?” and one student answered, “It gets shorter,” which seems reasonable but is incorrect. I was able to explain that the doubling time stays the same even though the rate of reproduction (the number of new cells per second) increases rapidly.

Graph showing how the number of cells increases over time.
Switching from growth to decay (half-life of 50 sec).

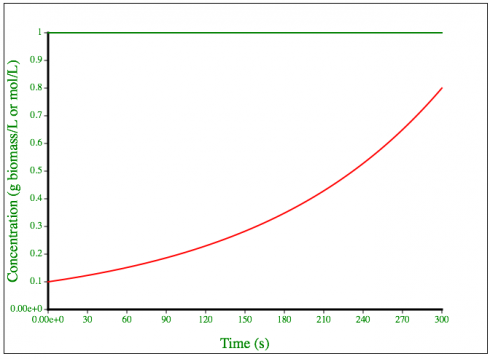
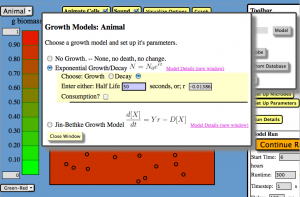
Then I changed the model from growth to decay by changing the doubling time to a half-life. Essentially this changes the coefficient in the exponent of the growth equation from positive to negative. The growth rate’s doubling time was 100 seconds, but I used a half life of 50 seconds for decay to accelerate things a bit, but still show the persistence of the last of the bugs.

Exponential decrease in cell population/biomass.

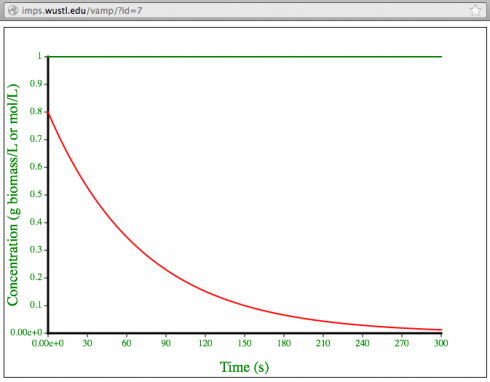
The cells died really fast in the beginning, and while there was just one cell was left at the very end, it was pretty clear just how persistent that last cell was; cells were dieing so slowly at the end.

This is similar to what happens when someone takes antibiotics. The typical course lasts for 10 days, but you’ve killed enough of the bacteria to loose the symptoms of sickness after two or three. Those final few that remain are the most resistant to the antibiotic, and if you don’t kill them then, once you stop taking the antibiotic, they’ll start to grow and replicate and you’ll end up sick again with a new, antibiotic-resistant population of bacteria.

I thought that using the VAMP model for the demonstration worked very well. The sound of the cells popping up faster and faster with exponential growth seemed to help amplify the visual effect, and make the whole thing more real. And during the decay phase, having that last cell hang on, seemingly forever, really helped convey the idea that bacteria can be extremely persistent.

Exponential Growth/Decay Models (Summary)

A quick summary (more details here):

The equation that describes exponential growth is:
Exponential Growth: N = N_0 e^{rt}

where:

  • N = number of cells (or concentration of biomass);
  • N0 = the starting number of cells;
  • r = the rate constant, which determines how fast growth occurs; and
  • t = time.

You can set the r value, but that’s a bit abstract so often these models will use the doubling time – the time it takes for the population (the number of cells, or whatever, to double). The doubling time (td) can be calculated from the equation above by:

t_d = \frac{\ln 2}{r}

or if you know the doubling time you can find r using:

r = \frac{\ln 2}{t_d}

Finally, note that the only difference between a growth model and a decay model is the sign on the exponent:

Exponential Decay: N = N_0 e^{-rt}

Decay models have a half-life — the time it takes for half the population to die or change into something else.