Tag: factors

Using the Binomial Cube in Algebra

Figuring out (a+b)3; with a binomial cube.

After working with the hundred-squares, ten-bars, and thousand-cubes to figure out how to add polynomials, we borrowed the binomial and trinomial cubes to practice multiplying out factors. It’s a physical way of showing factor multiplication.

Binomial Square

You can first look at the binomial cube in two-dimensions as a binomial square by just finding the area of the top layer of four blocks.

If you label the length of the side of the red block, a, and the length of the blue block, b, you can calculate the areas of the individual pieces simply by multiplying their lengths times their widths.

Looking from the top down, the top layer of the binomial cube is a binomial square.

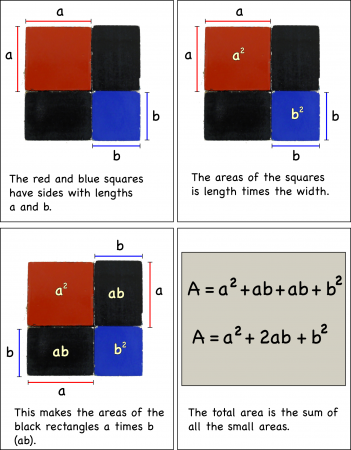
Adding up the individual areas you get the area of the entire square:

A = a^2 + 2ab + b^2

However, there is another way.

If you recognize that the length of each side of the entire square is equal to (a+b).

The length of each side of the cube is the sum of the lengths of the two squares.

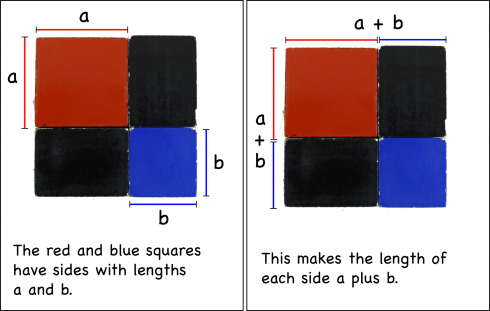
Then the total area is going to be total length (a+b) times the total width (a+b):

A = (a+b)^2 = (a+b)(a+b)

We can multiply this out (using FOIL is easiest):

(a+b)(a+b) = a^2 + ab + ab + b^2

which simplifies to give the same result as adding up the individual areas:

(a+b)^2 = a^2 + 2ab + b^2

The Binomial Cube

We can do the same thing using the entire cube by recognizing that the volume of the cube is the length times width times the depth, and all of these dimensions are the same: (a+b).

Using the full binomial cube.

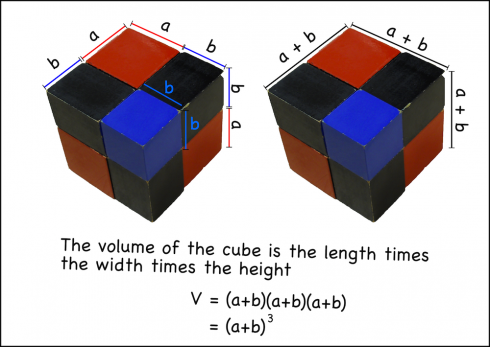
Now the students can go through the same process of multiplying out the factors, and can check their work be seeing if they get the same number of pieces (and dimensions) as the physical cube.

Success!