[Michael Bay] earns approximately 3.2 million $ for every explosion in his movies and a Michael Bay movie without explosions would earn 154.4 million $. This means that if Michael Bay wants to make a movie that earns more than Avatar’s 2781.5 million $ he has to have 817 explosions in his movie.
— Reddit:User:Mike-Dane: Math and Movies on Imgur.com.
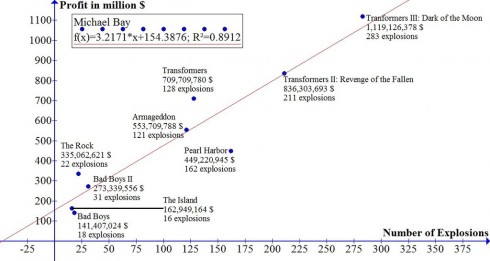
Reddit user Mike-Dane put together these entertaining linear regressions of a couple directors’ movie statistics. They’re a great way of showing algebra, pre-algebra, and pre-calculus students how to interpret graphs, and a somewhat whimsical way of showing how math can be applied to the fields of art and business.
Linear regression matches the best fit straight-line equations to data. The general equation for a straight line is:
y = mx + b
where m is the slope of the line — how fast in increases or decreases == and b is the intercept on the y-axis — which gives the initial value of the function.
So, for example, the Micheal Bay, profits vs. explosions, linear equation is:
Profit (in $millions) = 3.2 × (# of explosions) + 154
which means that a Michael Bay movie with no explosions (where # of explosions= 0) would make $154 million. And every additional explosion in a movie adds $3.2 million to the profits.
Furthermore, the regression coefficient (R2) of 0.89 shows that this equation is a pretty good match to the data.
Mike-Dane gets an even better regression coefficient (R2 = 0.97) when he compares the quality of M. Night Shyamalan over time.
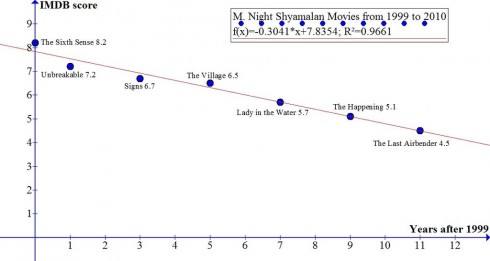
In this graph the linear regression equation is:
Movie Score = -0.3014 × (year after 1999) + 7.8354
This equations suggests that the quality of Shyamalan’s movies decreases (notice the negative sign in the equation) by 0.3014 points every year. If you wanted to, you could, using some basic algebra, determine when he’d score a 0.