Middle and High School … from a Montessori Point of View
Dr. Klaus Schmitt has some utterly amazing photographs that simulate what bees and butterflies can see. They can see ultra-violet wavelengths of light, which we can’t.
Schmitt maps the ultra-violet in the image to blue to make it visible to our eyes.
His site (Photography of the Invisible World (updated)) has a lot more pictures and information about the process.
The eye’s lens is pretty good at blocking ultra-violet light, so when Claude Monet (whose works we visited earlier this year) had the lens of his eye removed he could see a little into the ultra-violet wavelengths of light.
Monet’s story is in a free iPad book put out by the Exploratorium of San Francisco called Color Uncovered (which I have to get). Carl Zimmer has a review that includes more details about Monet and how the eye works.
P.S.: All of Monet’s works can be found on WikiPaintings, a great resource for electronic copies of old paintings (that are out of copyright).
The Guardian has an excellent video that explains how the images from the Hubble Space Telescope are created.
Each image from most research telescopes only capture certain, specific colors (wavelengths of light). One camera might only capture red light, another blue, and another green. These are captured in black and white, with black indicating no light and white the full intensity of light at that wavelength. Since red, blue and green are the primary colors, they can be mixed to compose the spectacular images of stars, galaxies, and the universe that NASA puts out every day.
The process looks something like this:
NASA’s image of the day is always worth a look.
I’ve been using the command line program SoX to generate tones for my physics demonstrations on sound waves.
Single frequency tones can be used for talking about frequency and wavelength, as well as discussing octaves.
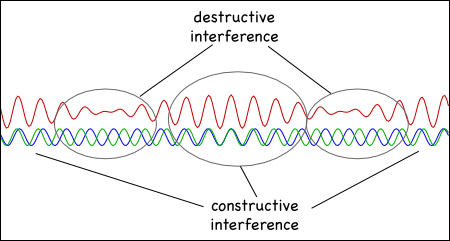
Combine two tones allows you to talk about interference and beats.
SoX can do a lot more than this, so I though I’d compile what I’m using it for in a single, reference post. For the record: I’m using SoX in Terminal on a Mac.
To play a single note (frequency 173.5 Hz) for 5 seconds, use:
> play -n synth 5 sin 347
To save the note to a mp3 file (called note.mp3) use:
> sox -n note.mp3 synth 5 sin 347
The SoX command to play two notes with frequencies of 347 and 357 Hz is:
> play -n synth 15 sin 347 sin 357
and to make an mp3 file use:
> sox -n beat_10.mp3 synth 15 sin 347 sin 357
Play two sound tones that are close together in frequency and the sound waves will overlap to create a kind of oscillating sound called a beat.
Below are two tones: separated and then mixed — listen for the beat.
| Frequency | Sound File (mp3) | |
|---|---|---|
| Tone 1 | 347 Hz | 1m.mpg |
| Tone 2 | 357 Hz | 1m-357.mp3 |
| Mixed Tones (with beat) | 347 Hz + 357 Hz | beat_10.mp3 |
Interestingly, you can sometimes hear the beat as a third tone if the frequency difference is just right. The frequency of the beat is the difference between the frequency of the two tones.
The SoX command to play two notes with frequencies of 347 and 357 Hz is:
> play -n synth 15 sin 347 sin 357
to make an mp3 file use:
> sox -n beat_10.mp3 synth 15 sin 347 sin 357
I’ve not had much real musical training, but enough to know that I have a terrible ear for sound and can’t reproduce a note for anything. However, an informed source tells me that octaves represent the same note at different pitches.
The pitch is the frequency of the sound wave.
If one note has twice the frequency of the other, they’re said to be one octave apart. For example, click on the image below to listen to the same note at different octaves:
Or play the files:
| Wavelength | Frequency | Sound File (mp3) |
|---|---|---|
| 1 m | 347 Hz | 1m.mpg |
| 0.5 m | 694 Hz | 50cm.mp3 |
| 0.25 m | 1388 Hz | 25cm.mp3 |
One of my students asked, “How black can you get?” I didn’t know the answer; however, serendipitously, I ran into this article last night. Researchers in Rochester, NY have created a solar cell that absorbs 99.7% of incoming light, which means that it has an albedo (reflectivity) of just 0.3%. Since solar cells create energy by absorbing light, the more light it can absorb — the blacker the solar cell — the more efficient the solar cell is likely to be.
I put together a VPython model to interactively illustrate how ray diagrams can be used to determine the appearance of an object in a concave, parabolic mirror. The video below demonstrates, but the code can be found here.
The white arrow is the object, and the yellow arrow shows it apparent magnification and orientation. You can drag the arrow around by its base, or make it taller (or shorter) by dragging the tip of the arrow up and down.
When the object is closer to the mirror than the mirror’s focal distance then the object appears enlarged.
When the object is between 1 and 2 focal distances away from the lens, it still appears enlarged, but is upside down. (Note that at one focal distance away the object disappears entirely from the mirror.)
At twice the focal distance the object appears to be the same size but upside down.
Beyond 2 times the focal distance the object appears upside down and shrunken.
NOTE: To create images from VPython, and then convert them into a movie, I used this technique.