Tag: quadratics

Solving Quadratics

Solving quadratic equations requires finding the factors, which is not nearly as easy as multiplying out the factors to get the unfactored equation.

Instead, you have to do a bit of trial and error, to figure out which pairs of numbers multiply to give the constant in the equation and then add together to give the coefficient of the x term.

Factoring quadratic equations.

It gets easier with practice. Or you could use the quadratic formula, where if the equation were:

a x^2 + b x + c = 0

The solutions would be found with:

x=\frac{-b \pm \sqrt {b^2-4ac}}{2a}

So in the equation used in the diagram:
x^2 + 7 x + 10 = 0

you get:

  • a = 1
  • b = 7
  • c = 10

Putting these values into the quadratic equation gives:

x=\frac{-7 \pm \sqrt {7^2-4(1)(10)}}{2(1)}

which simplifies to:

x=\frac{-7 \pm \sqrt {49-40}}{2}

x=\frac{-7 \pm \sqrt {9}}{2}

x=\frac{-7 \pm 3}{2}

With the whole plus-or-minus thing (\pm), this last equation gives two solutions:

(1): x=\frac{-7 + 3}{2} = -5

and,

(2): x=\frac{-7 - 3}{2} = -2

Now, you may have noticed that the solutions are negative, but when the equation is factored in the illustration, the result is:

(x + 5) (x + 2) = 0

The difference is that, although we’ve factored the equation, we have not solved it. When I say solve the equation, I mean find the values of x that would result in the left hand side of the equation being equal to the right, which is zero. Since multiplying anything by zero will give you zero, and the two factors multiply each other, the left-hand-side of the equation will equal zero when either one of the two factors equals zero.

So:


(x + 5) = 0
x = – 5

and:


(x + 2) = 0
x = -2

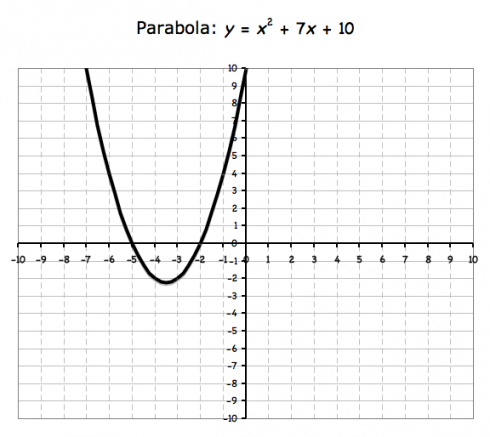
Finally, we can plot the line:

y = x^2 + 7 x + 10

using the Graphing Calculator Pro app, or this somewhat crude Parabola-Line Excel Graphing Worksheet, to show that the line crosses the x axis at -5 and -2.:

Note the curve crosses the x axis at -5 and -2.

Illustrating the Multiplication of Quadratic Factors

Each term needs to multiply the other two terms in the opposite parenthesis, so start with the reds, then do the two mixed colors, then the blues, and finally, combine the mixed colors.

I’ve been playing around with ways of showing how to multiply out quadratic factors like the one above. I’m still not perfectly happy with these animations but they’re the best I’ve come up with so far. A smoother, Flash or svg animation might work better though.

In this second version the terms being multiplied are highlighted. I like how the highlighting gives some more stability to the animation, but I’m always leery of putting too much color or bells and whistles because they tend to complicate the picture. In this case at least, I think all the colors have meaning and are useful.

Multiplication of quadratic factors.