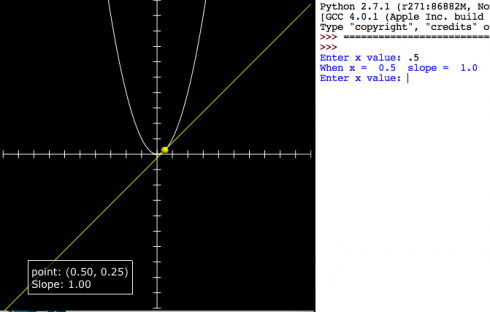
This quick program is intended to introduce differentiation as a way of finding the slope of a line. Students know how to find the slope of a tangent line at least conceptually (by drawing). We pick a curve: in this case:
![]()
then enter values of x in the program to see how x, the function value and the differential compare to each other.
| x | f(x) | f'(x) |
|---|---|---|
| 0.5 | 0.25 | 1 |
| 1 | 1 | 2 |
| 2 | 2 | 4 |
| 3 | 9 | 6 |
Because it’s quick you have to change the function in the code, and enter the values for x in the python shell.
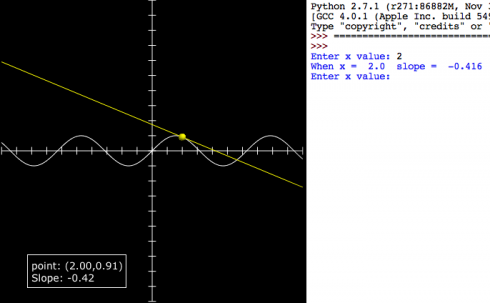
differentiation_intro_numeric.py
from visual import *
class tangent_line:
def __init__(self):
self.dx = 0.1
self.line = curve()
self.tangent_line = curve()
self.point = sphere(radius=.25,color=color.yellow)
self.point.visible = False
self.label = label(pos=(-5,-8))
'''CHANGE FUNCTION (y) HERE'''
# the original function
def f(self, x):
#y = sin(x)
y = x**2
return y
'''END CHANGE FUNCTION HERE'''
def find_slope(self, x):
sdx = .00001
m = (self.f(x+sdx)-self.f(x))/sdx
return round(m,3)
def draw(self):
for x in arange(xmin, xmax+self.dx, self.dx):
self.line.append(pos=(x, self.f(x)))
def draw_tangent(self, x):
m = self.find_slope(x)
y = self.f(x)
b = y - m * x
print "When x = ", x, " slope = ", m
self.label.text = "point: (%1.2f, %1.2f)\nSlope: %1.2f" % (x,y,m)
self.plot_point(x)
#draw tangent
self.tangent_line.visible = False
self.tangent_line = curve(pos=[(xmin,m*xmin+b),(xmax,m*xmax+b)], color=color.yellow)
def plot_point(self, x):
self.point.visible = True
self.point.pos = (x, self.f(x))
#axes
xmin = -10.
xmax = 10.
ymin = -10.
ymax = 10.
xaxis = curve(pos=[(xmin,0),(xmax,0)])
yaxis = curve(pos=[(0,ymin),(0,ymax)])
#tick marks
tic_dx = 1.0
tic_h = .5
for i in arange(xmin,xmax+tic_dx,tic_dx):
tic = curve(pos=[(i,-0.5*tic_h),(i,0.5*tic_h)])
for i in arange(ymin,ymax+tic_dx,tic_dx):
tic = curve(pos=[(-0.5*tic_h,i),(0.5*tic_h,i)])
#stop scene from zooming out too far when the curve is drawn
scene.autoscale = False
# draw curve
func = tangent_line()
func.draw()
# get input
while 1:
xin = raw_input("Enter x value: ")
func.draw_tangent(float(xin))