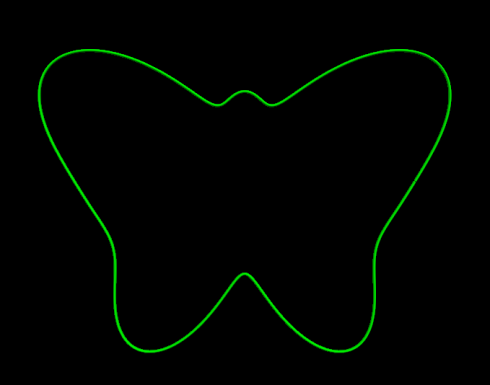
I was looking for mathematical functions I could use to shape guitar bodies, and I came across Hubpages’ user calculus-geometry‘s beautiful page on how to generate butterfly outlines using functions in polar coordinates.
The butterfly above was generated using the function:
r(θ) = 12 – sin(θ) + 2 sin(3θ) + 2 sin(5θ) – sin(7θ) + 3 cos(2θ) – 2 cos(4θ)
The code I used (using VPython) is:
from visual import *
''' the main function '''
def r(theta):
#r = 1+cos(theta)
#Archimides' sprial
#r = 0.5*(theta)
#heart: http://jwilson.coe.uga.edu/EMT669/Essay.ideas/Heart/Hearts.html
#r = 5*sin(theta) - sin(5*theta)
#butterfly: http://calculus-geometry.hubpages.com/hub/Butterfly-Curves-in-Polar-Coordinates-on-a-Graphing-Calculator
#r = 8-sin(theta)+2*sin(3*theta)+2*sin(5*theta)-sin(7*theta)+3*cos(2*theta)-2*cos(4*theta)
r = 12-sin(theta)+2*sin(3*theta)+2*sin(5*theta)-sin(7*theta)+3*cos(2*theta)-2*cos(4*theta)
return r
'''convert to rectangular coordinates'''
def xy(r, theta):
x = r * cos(theta)
y = r * sin(theta)
return vector(x, y)
path = curve(color=color.green, radius=.2)
theta = 0.0
print pi, theta, r(theta) , xy(r(theta), theta)
while theta <= 2*pi:
rate(100)
theta += 0.01
path.append(pos=xy(r(theta), theta))