waves – Montessori Muddle

The Math of Music

Mark French has an excellent YouTube channel on Mechanical Engineering, including the above video on Math and Music. The video describes the mathematical relationships between musical notes.

Given the sequence of notes: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C.

Let the frequency of the C note be f₀, the frequency of C# be f₁ etc.

The ratio of any two successive frequencies is constant (r). For example:

$\frac{f_1}{f_0} = r$

so:

$\frac{f_1}{f_0} = \frac{f_2}{f_1} = \frac{f_4}{f_3} = \frac{f_{12}}{f_{11}} = r$

We can find the ratio of the first and third notes by combining the first two ratios. First solve for f₁ in the first equation:

$\frac{f_1}{f_0} = r$

solving for f₁,

$f_1 = f_0 \; r$

now take the second ratio:

$\frac{f_2}{f_1} = r$

and substitute for f₁,

$\frac{f_2}{f_0 \; r} = r$

which gives:

$\frac{f_2}{f_0} = r^2$

We can now generalize to get the formula:

$\frac{f_n}{f_0} = r^n$

or

$f_n = f_0 \; r^n$

where,

n – is the number of the note

From this we can see that comparing the ratio of the first and last notes (f₁₂/f₀) is:

$\frac{f_{12}}{f_0} = r^{12}$

Now, as we’ve seen before, when we talked about octaves, the frequency of the same note in two different octaves is a factor of two times the lower octave note.

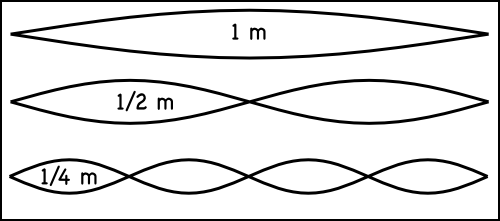
Harmonic_octaves — Click the waves to hear the different octaves. The wavelengths of the sounds are shown (in meters).

So, the frequency ratio between the first C (f₀) and the second C (f₁₂) is 2:

$\frac{f_{12}}{f_0} = 2$

therefore:

$\frac{f_{12}}{f_0} = 2 = r^{12}$

so we can now find r:

$r^{12} = 2$

$r = \sqrt[12]{2}$

Finally, we can now find the frequency of all the notes if we know that the international standard for the note A4 is 440 Hz.

Mark French has details on the math in his two books: Engineering the Guitar which is algebra based, and Technology of the Guitar, which is calculus based.

We talked about waves today down at the creek. The water was fairly calm so we could make some nice surface waves using floating leaves to show the up-down/side-to-side motion as the waves passed. I gave them 10 minutes to “play”, and more than one team tried to make a tsunami.

Since it’s allergy season, one student who could not go outside, read the chapter on the characteristics of waves and prepared a short–5 minutes–presentation for the rest of the class when we came back in.

Annotated image highlighting the crests of the waves and the wavelength.

The Rolling Shutter Effect

When you pluck a guitar string, the string moves up and down really fast. However, if you take a video of it with a digital camera with a rolling shutter (which most cameras have at the moment) it captures the motion of the string in a wavelike pattern that is proportional to the frequency of the motion of the string; the smaller strings move faster, create a higher pitched sound, and shows up as shorter-wavelength waves. Note: this is not the way the strings actually move, it’s an interesting, and potentially useful optical effect.

Because the optical effect really makes it look like there are a lot of internal waves rolling along the string — which there are not — I’d be quite cautious about using this in physics class. However, if a student wanted to go into the detail to understand how it works — and then explain it to the class, they can start with the math about standing waves in instrument strings and the relationship between sound pitch and wave motion, and a visual explanation of the rolling shutter effect:

The Physics of How Microwaves Work

An excellent explanation of how microwaves work. It talks about waves (how to determine the frequency and wavelength of microwaves), electricity (magnetrons), heat and temperature.

Resonance Frequencies: MythBusters investigate Tesla’s Earthquake Machine

The whole episode is worth watching, but this little section (at 10:52) of MythBusters’ attempt to build an earthquake machine there demonstrate the resonance frequency in a water tank provides a nice visualization.

Iridescent Wings – The Physics

irridescent-4978 — The bright blue iridescence of the wings of this insect results from the way light refracts through the thin layered membranes of the wings.

When you look at the sunlight reflected off this black insect’s wings at just the right angle, they blaze bright blue. The phenomena is called iridescence, and results from the way different wavelengths of light refract through the wing membrane. Blue light is of just the right wavelength that the light reflected off the top of the membrane and the light that’s refracted through the membrane constructively interfere. The Natural Photonics program at the University of Exeter has an excellent page detailing the physics of iridescence in butterflies (Lepidoptera), and the history of the study of the subject.

Why are Earth’s Sunsets Red While Mars’ are Blue?

marspath_ss24_1 — The area around the Sun is blue on Mars because the gasses in the thin atmosphere don't scatter much, but the Martian dust does (it scatters the red). Image via NASA.

The dust in Mars’ atmosphere scatters red, while the major gasses in Earth’s atmosphere (Nitrogen and Oxygen) scatter blue light. Longer wavelengths of light, like red, will bounce off (scatter) larger particles like dust, while shorter wavelengths, like blue light, will bounce of smaller particles, like the molecules of gas in the atmosphere. The phenomena is called Rayleigh scattering, and is different from the mechanism where different molecules absorb different wavelengths of light.

Ezra Block and Robert Krulwich go into details on NPR.

ny-2-39-f60 — Blue sky in the upper right, but the dust scatters the red light.

Ultra-Violet Vision: Seeing like the Butterflies and the Bees

vis-uv-flower — Visible light (what we see) versus including ultra-violet light (what the bees see). Images by Klaus Schmitt: http://www.pbase.com/kds315/uv_photos

Dr. Klaus Schmitt has some utterly amazing photographs that simulate what bees and butterflies can see. They can see ultra-violet wavelengths of light, which we can’t.

Schmitt maps the ultra-violet in the image to blue to make it visible to our eyes.

His site (Photography of the Invisible World (updated)) has a lot more pictures and information about the process.

Tag: waves