Abstract
I punched a small hole (about 1mm radius) in a one gallon plastic bottle and had my students measure the rate at which water drained. Even though the apparatus and measurement technique was fairly rough, we were able to, with a little calculus, determine the equation for the height of the water in the bottle as a function of time.

Introduction
Questions about water draining from a tank are a pretty common in calculus textbooks, but there is a significant difference between seeing the problem written down, and having to figure it out from a physical example. The latter is much more challenging because it does not presuppose any relationships for the change in the height of water with time; students must determine the relationship from the data they collect.
The experimental approach mimics the challenges faced by scientists such as Henry Darcy who first determined the formulas for groundwater flow (Darcy, 1733) almost 300 years ago, not long after the development of modern calculus by Newton and Leibniz (O’Conner and Robertson, 1996).
Procedure

I punched a small hole, about 1mm in radius, in the base of a plastic, one-gallon bottle. I chose this particular type of bottle because the bulk of it was cylindrical in shape.
Students were instructed to figure out how the rate at which water flowed out (outflow rate) changed with time, and how the height of the water (h) in the bottle changed with time. These relationships would allow me to predict the outflow rate at any time, as well as how much water was left in the container at any time.
Data collection:
- To measure height versus time, we marked the side of the bottle (within the cylindrical region) in one centimeter increments and recorded the time it took for the water level to drop from one mark to the next. There were a total of 11 marks.
- To measure the outflow rate, we intercepted the outflow using a 25 ml beaker (not shown in Figure 2), and measured the time it took to fill to the 25 ml mark.
Results
| Time elapsed since last measurement | Height of water in container | Time to fill 25ml beaker |
|---|---|---|
| Δt (s) | h (cm) | tf (s) |
| 0.0 | 11 | 6.4 |
| 45.5 | 10 | 7.1 |
| 52.3 | 9 | 8.5 |
| 43.1 | 8 | 7.1 |
| 56.1 | 7 | 7.8 |
| 60.6 | 6 | 8.3 |
| 57.6 | 5 | 8.9 |
| 65.0 | 4 | 9.9 |
| 72.8 | 3 | 11.2 |
| 76.7 | 2 | 13.0 |
| 91.1 | 1 | 14.8 |
| 122.0 | 0 | 17.3 |
Table 1: Outflow rate, water height change with time.
To analyze the data, we calculated the total time (the cumulative sum of the elapsed time since the previous measurement) and the outflow rate. The outflow rate is the change in volume with time:
![]()
So our data table becomes:
| Time | Height of water in container | Outflow rate |
|---|---|---|
| t (s) | h (cm) | dV/dt (ml/s) |
| 0.0 | 11 | 3.91 |
| 45.5 | 10 | 3.52 |
| 97.8 | 9 | 2.94 |
| 140.9 | 8 | 3.52 |
| 197 | 7 | 3.21 |
| 257 | 6 | 3.01 |
| 315.1 | 5 | 2.81 |
| 380.1 | 4 | 2.53 |
| 452.9 | 3 | 2.23 |
| 529.6 | 2 | 1.92 |
| 620.7 | 1 | 1.69 |
| 742.7 | 0 | 1.45 |
Table 2. Height of water and outflow rate of the bottle.
The graph of the height of the water with time shows a curve, although it is difficult to determine precisely what type of curve. My students started by trying to fit a quadratic equation to it, which should work as we’ll see in a minute.
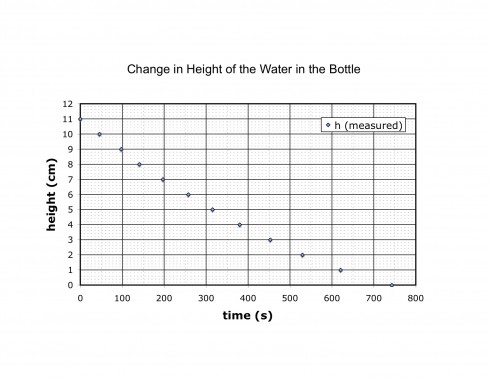
The plot of the outflow rate versus time, however, shows a pretty good linear trend. (Note that we do not use the first three datapoints (in Table 2), which we believe are erroneous because we were still sorting out the measuring method.)
Although I’ll note here that the data should ideally be modeled using a square root equation (Torricelli’s Law), that is beyond the present scope of the problem (we’ll try that tomorrow as a follow exercise).
Plotting the data in Excel we could add a linear trendline.
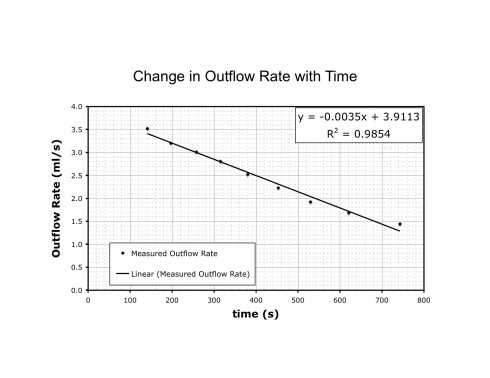
For the linear trendline, Excel gives the equation:
![]()
The y-axis is outflow rate (the change in volume with time), and the x axis is time (t), so the linear equation becomes:
![]()
Notice that this is a differential equation.
To determine the rate of at which the height of water in the container is changing, we need to recognize that the container is cylindrical in shape, and the volume (V) of a cylinder depends on its radius (r) and height (h):
![]()
which can be substituted into differential in the rate equation:
![]()
since π and the radius (r) are constants (since the jug’s shape is a cylinder), they can be pulled out of the differential:
![]()
Dividing through by πr2 solves for the rate of change of height:
![]()
Isolating the coefficients gives:
![]()
This equation should give the rate at which the height changes with time, however, if you look at it carefully you’ll realize that for the time range we’re using (less than 800 seconds) the value of dh/dt will always be positive. We correct this by recognizing that the outflow rate is a loss of water, so a positive outflow should result in a negative change in height, therefore we rewrite the equation as:
![]()
which gives:
![]()
Now comes the calculus
Now, we can use this rate equation to find the equation for height versus time by integrating with respect to time:
![]()
to get:
![]()
And all we have to do to the find the constant of integration is substitute in a known point, an initial value. As is often the case, the best point to use is the starting point where t=0 makes the rest of the calculations easier. In our case, when t=0, h=11:
![]()
so:
![]()
And our final equation becomes:
![]()
which is a quadratic equation as my students guessed before we did the calculus.
Does it work?
You will notice that in the math above, we never use the height data in determining equation for height versus time; all the calculations are based on the trendline for the outflow rate versus time.
As a result, we can compare the results of our equation to the actual measurements to see if our calculations are even close. Remarkably, they are.
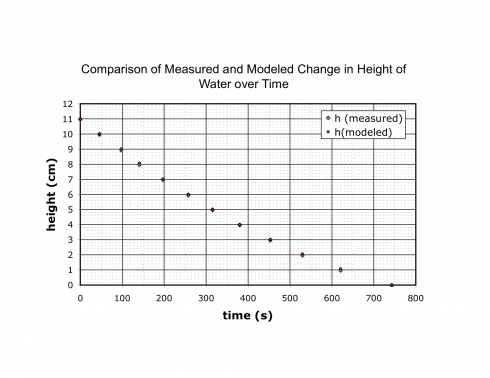
Discussion
Despite all the potential for error, particularly, our relatively crude measurement techniques, and the imperfect cylindrical shape of our plastic bottle, the experiment went remarkably well.
Students found it quite challenging, and required some assistance even though this is a problem they have seen before in their textbook.
The problems in the textbook use Torricelli’s Law, which should much better describe the draining of a tank than the linear equation we find for dV/dt.
Torricelli’s Law:
![]()
where a is the area of the outlet hole, and g is the acceleration due to gravity.
In our actual experiment it is difficult to tell that a square root function would work better. Excel does not have an option for matching a square root function, so the calculations would become more involved (although it could be set up using Excel’s iterative solver or Goal Seek function).
Conclusion
Our experiment to use calculus to determine the rate of change of the height of water in a leaking plastic water bottle was a successful exercise even though the roughness of the data collection did not permit identification of the square root law for leakage.