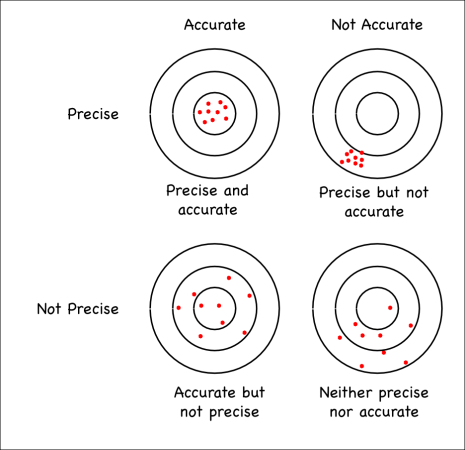
It’s possible to be precise but not accurate. It’s also possible to be accurate but not precise. These ideas are summarized very nicely in this diagram.
Middle and High School … from a Montessori Point of View
When it comes to particle physics … [m]easuring something once is meaningless because of the high degree of uncertainty involved in such exotic, small systems. Scientists rely on taking measurements over and over again — enough times to dismiss the chance of a fluke.
— Moskowitz (2011): Is the New Physics Here? Atom Smashers Get an Antimatter Surprise in LiveScience
New research, out of the Large Haldron Collider in Switzerland, shows a 0.8% difference in the way matter and antimatter particles behave. This small difference could go a long way in explaining why the universe is made up mostly of matter today, even though in the beginning there were about equal amounts of matter and antimatter. It would mean that the current, best theory describing particle physics, the Standard Model, needs some significant tweaking.

0.8% is small, but significant. How confident are the physicists that their measurements are accurate? Well, the more measurements you take the more confident you can be in your average result, though you can never be 100% certain. The LHC scientists did enough measurements that they could calculate, statistically, that there is only a 0.05% chance that their measurement is wrong.

I did a little exercise at the start of my high-school physics class today that introduced different types of experimental error. We’re starting the second quarter now and it’s time for their lab reports to including more discussion about potential sources of error, how they might fix some of them, and what they might mean.
One of the stairwells just outside the physics classroom wraps around nicely, so students could stand on the steps and, using stopwatches, time it as I dropped a tennis ball 5.3 meters, from the top banister to the floor below.

They had a variety of stopwatches, including a number of phones, at least one wristwatch, and a few of the classroom stopwatches that I had on hand. Some devices could do readings to one hundredth of a second, while others could only do tenths of a second. So you can see that there is some error just due to how detailed the measuring device can be read. We’ll call this the reading error. If the best value your stopwatch gives you is to the tenth of a second, then you have a reading error of plus or minus 0.1 seconds (±0.1 s). And you can’t do much about this other than get a better measuring device.
Another source of error is just due to random differences that will happen with every experimental trial. Maybe you were just a fraction of a second slower stopping your watch this time compared to the last. Maybe a slight gust of air slowed the balls fall when it dropped this time. This type of error is usually just called random error, and can only be reduced by taking more and more measurements.
Our combination of reading and random errors, meant that we had quite a wide range of results – ranging from a minimum time of 0.7 seconds, to a maximum of 1.2 seconds.
So what was the right answer?
Well, you can calculate the falling time if you know the distance (d) the ball fell (d = 5.3 m), and its acceleration due to gravity (g = 9.8 m/s2) using the equation:
![]()
which gives:
![]()
So while some individual measurements were off by over 30%, the average value was off by only 8%, which is a nice illustration of the phenomenon that the more measurements you take, the better your result. In fact, you can plot the improvement in the data by drawing a graph of how the average of the measurements improves with the number of measurements (n) you take.

More measurements reduce the random error, but you tend to get to a point of diminishing returns when you average just does not improve enough to make it worth the effort of taking more measurements. The graph shows the average slowly ramping up after you use five measurements. While there are statistical techniques that can help you determine how many samples are enough, you ultimately have to base you decision on how accurate you want to be and how much time and energy you want to spend on the project. Given the large range of values we have in this example, I would not want to use less than six measurements.
But, as you can see from the graph, even with over a dozen measurements, the average measured value remains persistently lower than the calculated value. Why?
This is quite likely due to some systematic error in our experiment – an error you make every time you do the experiment. Systematic errors are the most interesting type of errors because they tell you that something in the way you’ve designed your experiment is faulty.
The most exciting type of systematic error would, in my opinion, be one caused by a fundamental error in your assumptions, because they challenge you to fundamentally reevaluate what you’re doing. The scientists who recently reported seeing particles moving faster than light made their discovery because there was a systematic error in their measurements – an error that may result in the rewriting of the laws of physics.
In our experiment, I calculated the time the tennis ball took to fall using the gravitational acceleration at the surface of the Earth (9.8 m/s2). One important force that I did not consider in the calculation was air resistance. Air resistance would slow down the ball every single time it was dropped. It would be a systematic error. In fact, we could use the error that shows up to actually calculate the force of the air resistance.
However, since air resistance would slow the ball down, it would take longer to hit the floor. Unfortunately, our measurements were shorter than the calculated falling time so air resistance is unlikely to explain our error. So we’re left with some error in how the experiment was done. And quite frankly, I’m not really sure what it is. I suspect it has to do with student’s reaction times – it probably took them longer to start their stopwatches when I dropped the ball than it did to stop them when the ball hit the floor – but I’m not sure. We’ll need further experiments to figure this one out.
On reflection, I think I probably would have done better using a less dense ball, perhaps a styrofoam ball, that would be more affected by air resistance, so I can show how systematic errors can be useful.
Fortunately (sort of) in my demonstration I made an error in calculating the falling rate – I forgot to include the 2 under the square root sign – so I ended up with a much lower predicted falling time for the ball – which allowed me to go through a whole exercise showing the class how to use Excel’s Goal Seek function to figure out the deceleration due to air resistance.
My Excel Spreadsheet with all the data and calculations is included here.
There are quite a number of other things that I did not get into since I was trying to keep this exercise short (less than half an hour), but one key one would be using significant figures.
There are a number of good, but technical websites dealing with error analysis including this, this and this.