Using this data for the decay of a radioisotope, find its half life.
| t (s) | A (g) |
| 0 | 100 |
| 100 | 56.65706876 |
| 200 | 32.10023441 |
| 300 | 18.18705188 |
| 400 | 10.30425049 |
| 500 | 5.838086287 |
| 600 | 3.307688562 |
We can start with the equation for decay based on the half life:
where:
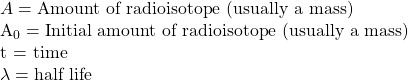
and linearize (make it so it can be plotted as a straight line) by using logarithms.
Take the log of each side (use base 2 because of the half life):Use the rules of logarithms to simplify:
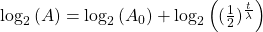
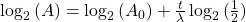
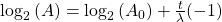
Finally rearrange a little:
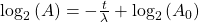
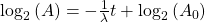
Now, since the two variables in the last equation are A and t we can see the analogy between this equation and the equation of a straight line:
and,
where:
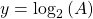
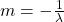
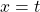
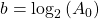
So if we draw a graph with log₂(A) on the y-axis, and time (t) on the x axis, the slope of the line should be:
Which we can use to find the half life (λ).