Year: 2012

Reasons to Study Algebra: Economics


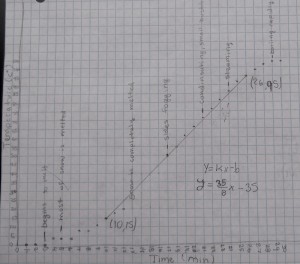
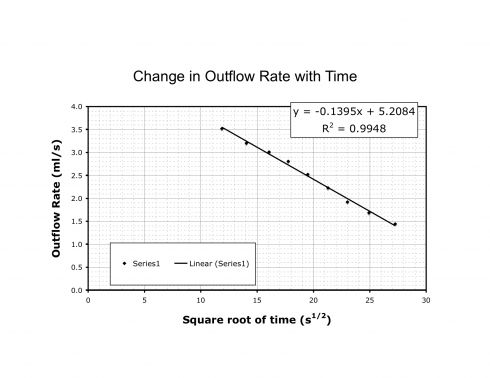
I hope you think that I am an acceptable writer, but when it comes to economics I speak English as a second language: I think in equations and diagrams, then translate.

— Krugman (1996): Economic Culture Wars in Slate

I sometimes get the question: Why do I have to learn algebra? Followed by the statement: I’m never going to have to use it again. My response is that it’s a bit like learning to read; you can survive in society being illiterate, but it’s not easy. The same goes for algebra, but it’s a little more complex.

Paul Krugman argues for the importance of algebra for anyone thinking about economics, the economy, and what to do about it. Even at the basic level, economists think in mathematical equations and algebraic models, then they have to translate their thoughts into English to communicate them. People who are not familiar with algebra are at a distinct advantage.

There are important ideas … that can be expressed in plain English, and there are plenty of fools doing fancy mathematical models. But there are also important ideas that are crystal clear if you can stand algebra, and very difficult to grasp if you can’t. [my emphasis] International trade in particular happens to be a subject in which a page or two of algebra and diagrams is worth 10 volumes of mere words. That is why it is the particular subfield of economics in which the views of those who understand the subject and those who do not diverge most sharply.

— Krugman (1996): Economic Culture Wars in Slate

P.S. In the article, he also points out the importance of algebra in the field of evolutionary biology.

Serious evolutionary theorists such as John Maynard Smith or William Hamilton, like serious economists, think largely in terms of mathematical models. Indeed, the introduction to Maynard Smith’s classic tract Evolutionary Genetics flatly declares, “If you can’t stand algebra, stay away from evolutionary biology.” There is a core set of crucial ideas in his subject that, because they involve the interaction of several different factors, can only be clearly understood by someone willing to sit still for a bit of math.

↬ Reddit

Teaching Math Backwards

Having just had the chance to teach the entire upper (secondary) school math curriculum, I’ve been doing a little bit of necessary reflection on how to help students get interested. One of the key things we learned in the Montessori training was just how much more students learn when they’re self-motivated about a topic.

The common theme among all these classes was the use of the math to construct models to better understand the relationships between different things.

Figure 1. The rising temperatures in the middle of the graph can be modeled with a straight line. Graph by A.F.

In Algebra I the focus is on linear models, like the one my middle schoolers drew from the results of their ice-melting experiment in science (see Figure 1). Another example (that I’ve not posted on yet) is calculating the density of liquids from a graph of volume and mass.

By the time they get to calculus they’re not just dealing with more complex functions, but they’re integrating and differentiating them to derive fundamental relationships.

Linearized graph of outflow rate versus the square root of time. From the draining water experiment.

h = \int \frac{dh}{dt} dt = \int \left( \frac{-0.1395}{\pi r^2} t^{1/2} + \frac{5.21}{\pi r^2} \right) dt

Unfortunately, you usually end up with useful applications at the end of the book (or the chapter).

I wonder if it would not be more effective to put the examples in at the beginning. Not just in a little box for, “Why this is useful,” but start with the problem and then introduce the math need to solve it. A bit, perhaps, like Garfunkel and Mumford’s op-ed suggestion for more “real-life problems” in math education.

The Adolescent Sleep Cycle

Bora Zivkovic compiles some information on how kids circadian rhythms change during adolescence, and advocates for later school starting hours.

He points out the interesting concept of chronotypes:

Everyone, from little children, through teens and young adults to elderly, belongs to one of the ‘chronotypes’. You can be a more or less extreme lark (phase-advanced, tend to wake up and fall asleep early), a more or less extreme owl (phase-delayed, tend to wake up and fall asleep late). You can be something in between – some kind of “median” (I don’t want to call this normal, because the whole spectrum is normal) chronotype.

— Zivkovic (2012): When Should School Start in the morning in Scientific American (blog).

And how your chronotype gets phase-delayed at puberty:

No matter where you are on these continua, once you hit puberty your clock will phase-delay. If you were an owl to begin with, you will become a more extreme owl for about a dozen years. If you are an extreme lark, you’ll be a less extreme lark. In the late 20s, your clock will gradually go back to your baseline chronotype and retain it for the rest of your life.

— Zivkovic (2012): When Should School Start in the morning in Scientific American (blog).

U.S. Senators’ 10th Grade Speeches

NPR presents the results of a Sunlight Foundation study that showed that U.S. senatorial speeches average at a 10th grade reading level. The maximum is about 16th grade (high school + 4 years of college), while the minimum is about 8th grade. The average is down one and a half grade levels from just 10 years ago.

Note that the U.S. constitution was written at an 18th grade level.

Networks versus Trees: Ways of Analyzing the World

Manuel Lima contrasts the traditional, hierarchical, view of the world (evolution’s tree of life for example) to a more network oriented perspective.

One interesting part is the interpretation of the history of science as having three phases, dealing with Problems of:

  • Simplicity: Early scientific efforts (17th-19th centuries) was focused on “simple” models of cause and effect — embodied perhaps in Newton’s Laws, where every force has an equal and opposite force.
  • Disorganized Complexity: Think early 20th century nuclear physics — Heisenberg’s uncertainty principle for example — where the connections between events are complicated and sort of random/probabilistic.
  • Organized Complexity: Systems science sees the interrelatedness of everything: ecologic food webs; the Internet; horizontal gene transfer across the limbs of the tree of life.

ᔥ RSA Animate ↬ The Dish