No Such Thing as Dark Matter – Montessori Muddle

We’ve not been able to detect dark matter yet. Natalie Wolchover explains summarizes theories that could explain the way the universe works without having dark matter.

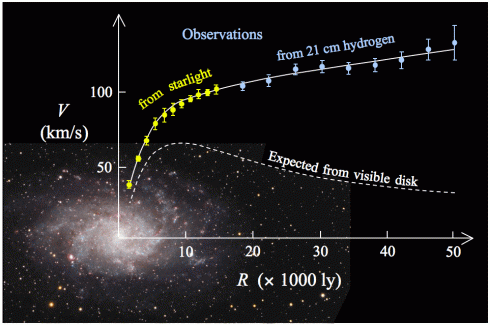
Key to it is the Modified Newtonian Dynamics (MOND) equation to explain why the stars at the outer edges of galaxies are moving faster than Newton’s force law predicts they should be.

Velocities of stars further away from the center of the galactic disk (larger R) have a higher velocity (V) than predicted by Newtonian physics. Dark matter has been used to explain this discrepancy, but tweaking the physics equations could do so as well. Image from Wikipedia.

Newton’s Second Law, finds that the Force (F) acting on an object is equal its mass (m) multiplied by its acceleration (a).

$F = m \cdot a$

The MOND equation adjusts this by adding in another multiplication factor (μ)

$F = \mu \cdot m \cdot a$

μ is just really close to 1 under “normal” everyday conditions, but gets bigger when accelerations are really, really small. Based on the evidence so far an equation for μ may be:

$\mu = \frac{a}{a_0} \frac{1}{\sqrt{1+\left(\frac{a}{a_0}\right)^2}}$

where, a₀ is a really, really small acceleration.

Factoring this μ factor into the equation for the force due to gravity ( $F_g$ ) changes it from:

$F_g = G \frac{ m_1 \cdot m_2}{r^2}$

into:

$F_g = G \frac{(m_1 \cdot m_2)}{r^2} + \frac{\sqrt{G \cdot \m_1 \cdot m_2 \cdot a_0}}{r}$

The key point is that in the first term, which is our standard version, the denominator is the radius squared ( $r^2$ ) while the second term has a plain radius denominator ( $r$ ).

This means as the distance between two objects gets larger, the first term decreases much faster and the second term becomes more important.

As a result, the gravitational pull between, say a star at the edge of a galaxy and the center of the galaxy, is not as small as the standard gravitational equation would predict it would be, and the stars a the edge of galaxies move faster than they would be predicted to be without the additional term.

References:

Leave a Reply