Linearizing an Exponential Function: Radioactive Decay

Using this data for the decay of a radioisotope, find its half life.

t (s)A (g)
0100
10056.65706876
20032.10023441
30018.18705188
40010.30425049
5005.838086287
6003.307688562

We can start with the equation for decay based on the half life:

   A = A_0 (\frac{1}{2})^\frac{t}{\lambda}  

 
where:
 A = \text{Amount of radioisotope (usually a mass)}  A_0 = \text{Initial amount of radioisotope (usually a mass)}   t = \text{time}  \lambda = \text{half life}

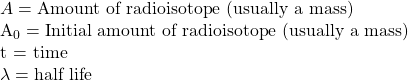
and linearize (make it so it can be plotted as a straight line) by using logarithms. 

Take the log of each side (use base 2 because of the half life):

  \log_2{(A)} = \log_2{  \left( A_0 (\frac{1}{2})^\frac{t}{\lambda} \right)} 

Use the rules of logarithms to simplify:

 \log_2{(A)} = \log_2{ ( A_0 )} + \log_2{  \left( (\frac{1}{2})^\frac{t}{\lambda} \right)}   

  \log_2{(A)} = \log_2{ ( A_0 )} +  \frac{t}{\lambda}  \log_2{   (\frac{1}{2}) }      

 \log_2{(A)} = \log_2{ ( A_0 )} +  \frac{t}{\lambda}  (-1)   

  \log_2{(A)} = \log_2{ ( A_0 )} -  \frac{t}{\lambda}       

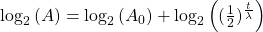
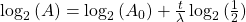
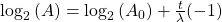
Finally rearrange a little:

  \log_2{(A)} =  -  \frac{t}{\lambda}  +  \log_2{ ( A_0 )}      

  \log_2{(A)} =  -  \frac{1}{\lambda} t +  \log_2{ ( A_0 )}

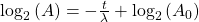
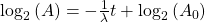
Now, since the two variables in the last equation are A and t we can see the analogy between this equation and the equation of a straight line:

 \log_2{(A)} =  -  \frac{1}{\lambda} t +  \log_2{ ( A_0 )}        

and,

   y =  m x +  b       

where:

   y = \log_2{(A)}        

   m =  -  \frac{1}{\lambda}        

   x = t       

   b =  \log_2{ ( A_0 )}

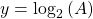
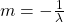
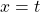
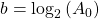
So if we draw a graph with log₂(A) on the y-axis, and time (t) on the x axis, the slope of the line should be:

   m =  -  \frac{1}{\lambda}

Which we can use to find the half life (λ).

Leave a Reply