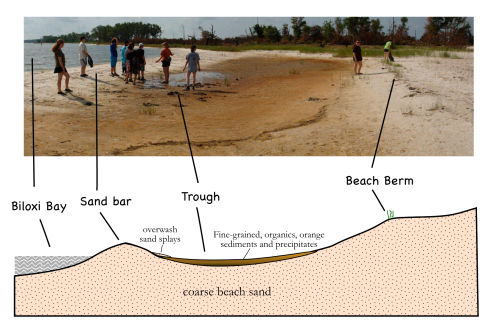
The western end of Deer Island extends a white, sandy, artificial, spit that partially covers the first of a series of riprap breakwaters that protect the waterfront development of the city of Biloxi. Although we’d landed there to pick up garbage as part of our coastal science camp, the beautifully developed beach profile was worth a few minutes.

The spit curves just ever so slightly northward, so it feels more of the direct force of waves blown all the way along the length of Biloxi Bay. The combination of unvegetated sand and stronger waves makes the beach along the spit looks very different from the beaches that parallel the shore. While the parallel beaches on Deer Island are covered in grass almost to the water’s edge (Fig. 2), the spit has a much wider beach, with a nicely developed sandbar protecting a shallow, flat-bottomed, water-saturated trough behind it (Fig. 1).
While the white beaches are pretty (that’s why they imported this sand after all), there are a number of fascinating features in the trough.

The first, and most obvious question is, why the reddish-orange color in the fine grained sediment at the bottom of the trough? A microscope and a little geochemical analysis would be useful here, however, lacking this equipment, we can try drawing parallels with some of our experiences in the past. In fact, we should remember seeing the same color in some of the streambeds when we were hiking in Natchez Trace State Park in Tennessee (Fig. 3). My best guess at that time was that the red was from iron in the groundwater being oxidized when it reached the surface.


This is probably not a bad guess for the red in the trough as well, since there is some fresh groundwater discharge from the shallow watertable on the island. However, I suspect that the story is a bit more complex, because the rich black color of the organic matter just beneath the surface (Fig. 4) suggest that the shallow water and surface sediment in the trough is lacking in oxygen. On the other hand, it’s not uncommon to have steep geochemical gradients in boundary environments like this one.
The physical and geochemical gradients extend horizontally as well as vertically. At the edges of the trough the organic matter just beneath the surface is green, not black (Fig. 5), because this is the color of the undecayed algae.
At the seaward side of the beach, the waves of Biloxi Bay lap against the sand bar. When the tide rises, and the wind picks up, these waves wash over the crest of the sand bar pushing water and sediment over the top into trough. When the sand washes evenly over the top it creates thin layers (possibly one layer with each high tide). If you cut into these layers you’ll see little the laminations in profile, which, because the layering is close to horizontal, look like the lines of topography on a map (Fig. 6). When the waves wash over small gaps in the sandbar the sediment it transports is deposited in a more concentrated area – these are called sand splays – that overlap and cover some of the fine-grained, orange sediment at the edge of the trough. These are both two of the small ways that the sand bar moves, slowly pushing inland.

Bioturbation
The features on the bottom of the trough are a quite interesting because of the observable effects of bioturbation (disturbance by organisms) (Figs. 7, 8 & 9).