A good NPR article based on a 2014 paper that finds that students who hand-write their notes have to think more about what they choose to write and so remember better than students who just transcribe lectures on their computers.
Category: audio
Necks, Fretboards, and Scale Length
Pluck a string on a guitar and the sound you hear depends on how fast it vibrates. The frequency is how many times it vibrates back and forth in each second. An A4 note has a frequency of 440 vibrations per second (one vibration per second is one Hertz).
The vibration frequency of a guitar string depends on three things:
- the mass of the string
- the tension on the string (how tight it’s pulled)
- and, the length of the string.
Guitar string sets come with wires of different masses. The guitar has little knobs on the end for adjusting the tension. For building the guitar, you have the most control over the last last parameter, the length of the string, which is called the scale length. Since the guitar string masses are pretty much set, and the strings can only hold so much tension, there are limits to the scale length you can choose for your guitar.
In a guitar, the scale length only refers to the length of the string that’s actually vibrating when you pluck the string, so it’s the distance between the nut and the bridge. For many guitars this turns out to be about 24.75 inches.

Frets
To play different notes, you shorten the vibrating length of the string by using your finger to hold down the string somewhere along the neck of the instrument. The fret board (which is attached to the neck) has a set of marks to help locate the fingering for the different notes. How do you determine where the fret marks are located?
Well, the music of math post showed how the frequency of different notes are related by a common ratio (r). With:
![]()
So given the notes:
| Note Number (n) | Note |
|---|---|
| 0 | C |
| 1 | C# |
| 2 | D |
| 3 | D# |
| 4 | E |
| 5 | F |
| 6 | F# |
| 7 | G |
| 8 | G# |
| 9 | A |
| 10 | A# |
| 11 | B |
| 12 | C |
Since the equation for the frequency of a note is:
![]()
we can find the length the string needs to be to play each note if we know the relationship between the frequency of the string (f) and the length of the string (l).
It turns out that the length is inversely proportional to the frequency.
![]()
So we can calculate the length of string for each note (ln) as a fraction of the scale length (Ls).
![]()
substituting for fn gives:
![]()
but since we know the length for f0 is the scale length (Ls) (that inverse relationship again):
![]()
giving:
When we play the different notes on the guitar, we move our fingers along the neck to shorten the vibrating parts of the string, so the base of the string stays at the same place–at the bridge. So, to mark where we need to place our fingers for each note, we put in marks at the right distance from the bridge. These marks are called frets, and we’ll call the distance from the bridge to each mark the fret distance (D_n). So we reformulate our formula to subtract the length of the vibrating string from the scale length of the guitar:

The fret marks are cut into a fret board that was supplied by the guitarbuilding team, which we glued onto the necks of our guitars. We did, however, have to add our own fret wire.

The team also has an activity for students to use a formula (a different one that’s recursive) to calculate the fret distance, but the Excel spreadsheet fret-spacing.xls can be used for reference (though it’s a good exercise for students to make their own).
The Math of Music
Mark French has an excellent YouTube channel on Mechanical Engineering, including the above video on Math and Music. The video describes the mathematical relationships between musical notes.
Given the sequence of notes: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C.
Let the frequency of the C note be f0, the frequency of C# be f1 etc.
The ratio of any two successive frequencies is constant (r). For example:
![]()
so:
![]()
We can find the ratio of the first and third notes by combining the first two ratios. First solve for f1 in the first equation:
![]()
solving for f1,
![]()
now take the second ratio:
![]()
and substitute for f1,
![]()
which gives:
![]()
We can now generalize to get the formula:
or
where,
- n – is the number of the note
From this we can see that comparing the ratio of the first and last notes (f12/f0) is:
![]()
Now, as we’ve seen before, when we talked about octaves, the frequency of the same note in two different octaves is a factor of two times the lower octave note.
So, the frequency ratio between the first C (f0) and the second C (f12) is 2:
![]()
therefore:
![]()
so we can now find r:
![]()
![]()
Finally, we can now find the frequency of all the notes if we know that the international standard for the note A4 is 440 Hz.
Mark French has details on the math in his two books: Engineering the Guitar which is algebra based, and Technology of the Guitar, which is calculus based.
Conflict over water
One of the articles my students brought to our Environmental Science discussion was about the growing fears about wars over water. Even within the U.S.A. there are significant conflicts, as demonstrated by this NPR article.
Texas has tried to buy Oklahoma water from the state, its cities and towns, and its Native American tribes. But Oklahoma lawmakers have blocked those efforts with a string of laws restricting out-of-state water exports.
The view in Texas is that Oklahoma isn’t even using its full allocation of Red River water. Oklahomans respond that Texas hasn’t gotten serious enough about conservation.
“Our poor, poor thirsty people in Dallas, Texas,” muses state Sen. Jerry Ellis, a Democrat who represents southeastern Oklahoma. “There’s nobody thirsty in Dallas, Texas.”
— Wertz,J., 2013: Thirsty States Take Water Battle To Supreme Court on NPR.
The full article:
P.S. Lauren Markham has an article about environmental “refugees” forced to leave Ethiopia because of the changing rainfall patterns over the last eight years.
Listen for the Beat

Play two sound tones that are close together in frequency and the sound waves will overlap to create a kind of oscillating sound called a beat.
Below are two tones: separated and then mixed — listen for the beat.
| Frequency | Sound File (mp3) | |
|---|---|---|
| Tone 1 | 347 Hz | 1m.mpg |
| Tone 2 | 357 Hz | 1m-357.mp3 |
| Mixed Tones (with beat) | 347 Hz + 357 Hz | beat_10.mp3 |
Interestingly, you can sometimes hear the beat as a third tone if the frequency difference is just right. The frequency of the beat is the difference between the frequency of the two tones.
Notes
The SoX command to play two notes with frequencies of 347 and 357 Hz is:
> play -n synth 15 sin 347 sin 357
to make an mp3 file use:
> sox -n beat_10.mp3 synth 15 sin 347 sin 357
Octave Sound Samples
I’ve not had much real musical training, but enough to know that I have a terrible ear for sound and can’t reproduce a note for anything. However, an informed source tells me that octaves represent the same note at different pitches.
The pitch is the frequency of the sound wave.
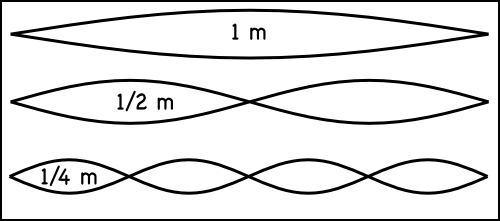
If one note has twice the frequency of the other, they’re said to be one octave apart. For example, click on the image below to listen to the same note at different octaves:

Or play the files:
| Wavelength | Frequency | Sound File (mp3) |
|---|---|---|
| 1 m | 347 Hz | 1m.mpg |
| 0.5 m | 694 Hz | 50cm.mp3 |
| 0.25 m | 1388 Hz | 25cm.mp3 |
Teaching Your Kids how to Argue
All that arguing with your teenager is, basically, teaching them how to argue. You yell, they learn to yell. You listen, and make your rational arguments respectfully, and they learn to do the same — both with you and with others; so much so that it inoculates against peer-pressure.
Patti Neighmond has a nice story about the benefits of parent-teenager arguments, on NPR’s All Things Considered. One particularly interesting is that adolescents who learn to argue well are much less susceptible to peer-pressure.
Facing the Advertising Noise

We face a lot of advertising. All the time. According to Martin Lindstrom, the author of Brandwashed, “the average American 3-year-old can recognize 100 brands” (NPR Staff, 2011). I usually discuss advertising at the same time as we’re talking about propaganda.
Guy Raz has an excellent interview with Lindstrom on All Things Considered.