Expectations of Math

Jonathan Wai wonders, “Why Is It Socially Acceptable To Be Bad At Math?” After all, it’s not socially acceptable to be illiterate.

The cultural norm that it’s okay to be bad at math has deleterious effects on student motivation. I’ve seen it myself. One parent of an excellent, hard-working student confessed that it was probably her talking about how bad she was at math that helped her kid feel like they didn’t need to work that hard at the subject; especially since the student didn’t think that they were going to use the math anyway.

Some think that the solution is to use a more integrated curriculum and teach, “a math curriculum that focused on real-life problems,”:

Imagine replacing the sequence of algebra, geometry and calculus with a sequence of finance, data and basic engineering. In the finance course, students would learn the exponential function, use formulas in spreadsheets and study the budgets of people, companies and governments. In the data course, students would gather their own data sets and learn how, in fields as diverse as sports and medicine, larger samples give better estimates of averages. In the basic engineering course, students would learn the workings of engines, sound waves, TV signals and computers. Science and math were originally discovered together, and they are best learned together now.

— Garfunkel and Mumford, 2011: How to Fix Our Math Education in the New York Times
— ↬ The Dish ↬ Finding the Next Einstein

Which seems like a good idea — more of an apprenticeship-style approach to math — but there still needs to be some space for the wonderful elegance of some of the apparently more abstract math. More real world applications could certainly be incorporated into the current curriculum, but it would be short-changing our students if we just left math for problem solving and did not delve a little into the principles behind the mathematical techniques they’re using in a more general way.

The Algebra of Straight Lines

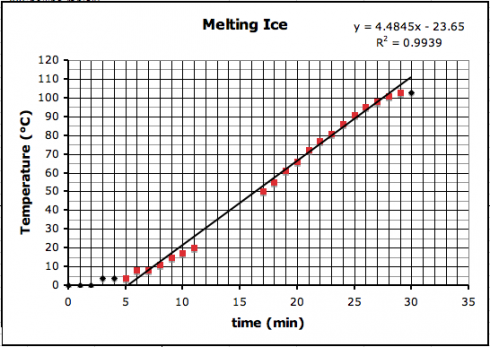
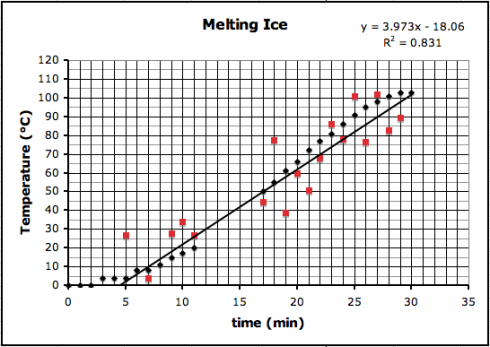
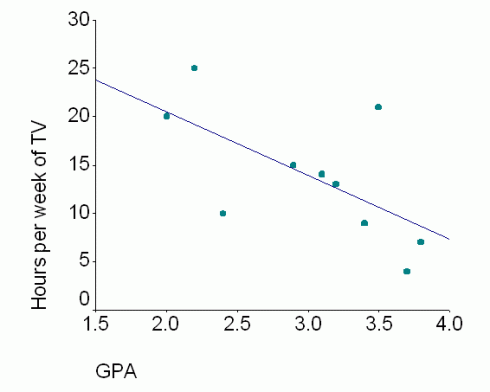
A quick graphical calculator for straight lines — based on This. It’s still incomplete, but it’s functional, and a useful complement to the equation of a straight line animation and the parabola graphing.

You can graph lines based on the equation of a line (in either the slope-intercept or point-slope forms), or from two points.

[inline]

Straight Lines

Slope-Intercept Form	Two Points	Point-Slope Form
`y = m x + b`	`(x₁, y₁) = ( , )`	`y – y₁ = m ( x – x₁)`
y = x +	`(x₂, y₂) = ( , )`	y – = ( x – )

x intercept:	Slope:	Equation:
y intercept:	Points:

[script type=”text/javascript”]

var width=500;
var height=500;
var xrange=10;
var yrange=10;

mx = width/(2.0*xrange);
bx = width/2.0;
my = -height/(2.0*yrange);
by = height/2.0;

document.getElementById(‘testing’).innerHTML = “Hello2”;

function draw_9359(ctx, polys) {

t_9359=t_9359+dt_9359;
//ctx.fillText (“t=”+t, xp(5), yp(5));
ctx.clearRect(0,0,width,height);

polys[0].drawAxes(ctx);
ctx.lineWidth=2;
polys[0].draw(ctx);

polys[0].write_eqn2(ctx);

//ctx.fillText (polys[0].get_parabola_vertex_form_eqn(), xp(5), yp(-5) );

// SHOW 2 POINTS USED TO CALCULATE LINE
if (show_2pts_ctrl_9359.checked==true) {
polys[0].circle_point(ctx, polys[0].p1.x, polys[0].p1.y, “#000”, 0.15);
polys[0].label_point_on_line(ctx, polys[0].p1.x, polys[0].p1.y);
polys[0].circle_point(ctx, polys[0].p2.x, polys[0].p2.y, “#000”, 0.15);
polys[0].label_point_on_line(ctx, polys[0].p2.x, polys[0].p2.y);

}

// SHOW Y INTERCEPT
if (show_y_intercept_ctrl_9359.checked==true) {
polys[0].draw_y_intercept_line(ctx);
document.getElementById(‘y_intercept_pos_9359’).innerHTML = “( 0 , “+ polys_9359[0].c.toPrecision(2)+ ” )”;

if (polys[0].b > 0.0) {
ctx.textAlign=”right”;
xoff = -0.5;
}
else {
ctx.textAlign=”left”;
xoff = 0.5;
}
ctx.fillText (‘y intercept: y = ‘+polys[0].c.toPrecision(2), xp(xoff), yp(polys_9359[0].c+0.25));

} else { document.getElementById(‘y_intercept_pos_9359’).innerHTML = “”;}

// SHOW SLOPE
if (show_slope_ctrl_9359.checked==true) {
polys[0].draw_slope_line(ctx);
document.getElementById(‘slope_pos_9359’).innerHTML = ” = “+polys[0].b.toPrecision(2);

} else { document.getElementById(‘slope_pos_9359’).innerHTML = “”;}

document.getElementById(‘slope_int_equation_9359’).innerHTML = polys[0].get_eqn2();

//SHOW INTERCEPTS
ctx.textAlign=”center”;
if (show_intercepts_ctrl_9359.checked==true) {
polys[0].x_intercepts(ctx);
if (polys[0].order == 2) {
if (polys[0].x_intcpts.length > 0) {
line = “0 = “;
for (var i=0; i 0.0) { sign=”-“;} else {sign=”+”;}
line = line + “(x “+sign+” “+ Math.abs(polys[0].x_intcpts[i].toPrecision(2))+ “)”;
}
ctx.fillText (line, xp(6), yp(7));
for (var i=0; i 0) {
if (polys[0].b > 0.0) {
ctx.textAlign=”right”;
xoff = -0.5;
}
else {
ctx.textAlign=”left”;
xoff = 0.5;
}
ctx.font = “12pt Calibri”;
ctx.fillStyle = “#00f”;
ctx.fillText (‘x intercept: x = ‘+polys[0].x_intcpts[0].toPrecision(2), xp(polys[0].x_intcpts[0]+xoff), yp(0.5));
document.getElementById(‘intercepts_pos_9359’).innerHTML = “( “+ polys[0].x_intcpts[0].toPrecision(2) + “, 0 )”;
}
else {
ctx.fillText (‘None’, xp(7), yp(7));
}

}

}
else {
document.getElementById(‘intercepts_pos_9359’).innerHTML = ” “;
}

// Finding the slope
outln = “

Finding the Slope

“;
outln += “

The slope of the line between the two points is the rise divided by the run: the change in elevation divided by the horizontal distance between the points.”;

// Write out intercept solution
outln = “

Finding the x-intercept

“;
outln += “

Start with the slope-intercept form of the equation:”;
outln += “

“+polys[0].get_eqn2(“y”,”x”,”html”)+”“;
outln += “

Know that at the x-intercept, y = 0 , which you substitute into the equation to get:”;
outln += “

“+polys[0].get_eqn2(“0″,”x”,”html”)+”“;
outln += “

Now move the b coefficient to the other side of the equation:”;
outln += “

“+(-polys[0].c).toPrecision(2)+” = “+ polys[0].b.toPrecision(2)+”x”+”“;
outln += “

And divide both sides by the slope to solve for x:”;
outln += “

“+(-polys[0].c).toPrecision(2)+ ” / “+ polys[0].b.toPrecision(2) + ” = “+ polys[0].b.toPrecision(2)+”x”+ ” / “+ polys[0].b.toPrecision(2)+”“;
outln += “

“+(-polys[0].c/polys[0].b).toPrecision(2)+” = “+”x”+”“;
outln += “

Therefore, the line intercepts the x axis at the point:”;
outln += “

( “+(-polys[0].c/polys[0].b).toPrecision(2)+” , 0 )”;
outln += “

When,”;
outln += “

“+”x = “+ (-polys[0].c/polys[0].b).toPrecision(2) +”“;

document.getElementById(‘x_intercept_9359’).innerHTML = outln;

//Write out the solution by factoring
solution = “

Finding the y-intercept

“;
if (polys[0].order == 2) {
solution = solution + “y = “+polys[0].a.toPrecision(2)+” x² “+polys[0].bsign+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;

solution = solution + ‘Factoring: ‘;

if (polys[0].x_intcpts.length > 0) {
solution = solution + ‘0 = ‘;
for (var i=0; i 0.0) { sign=”-“;} else {sign=”+”;}
solution = solution + “(x “+sign+” “+ Math.abs(polys[0].x_intcpts[i].toPrecision(2))+ “)”;
}
solution = solution + ‘

‘;
solution = solution + ‘Set each factor equal to zero:
‘;
for (var i=0; i 0.0) { sign=”-“;} else {sign=”+”;}
solution = solution + “x “+sign+” “+ Math.abs(polys[0].x_intcpts[i].toPrecision(2))+ ” = 0 “;
}
solution = solution + ‘

and solve for x:
‘;
for (var i=0; i‘;
}
document.getElementById(‘equation_9359’).innerHTML = solution;
}

else if (polys[0].order == 1) {
solution = solution + ‘

At the y-axis x = 0.
To find the y intercept, take the equation of the line, set x = 0, and solve for x.’;
solution = solution + ‘

‘;
solution = solution + “y = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;
solution = solution + ‘ ‘;
solution = solution + ” 0 = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;
solution = solution + ‘ ‘;
solution = solution + (-1.0*polys[0].c).toPrecision(2) +” = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+”

“;
solution = solution + ‘ ‘;
solution = solution + (-1.0*polys[0].c).toPrecision(2)+”/”+polys[0].b.toPrecision(2)+” = “+” x “+”

“;
solution = solution + ‘ ‘;
solution = solution + “x = “+ (-1.0*polys[0].c/polys[0].b).toPrecision(4)+”

“;

document.getElementById(‘equation_9359’).innerHTML = solution;

}

function update_form_9359 () {
b_coeff_9359.value = polys_9359[0].b+””;
c_coeff_9359.value = polys_9359[0].c+””;

y1_coeff_9359.value = polys_9359[0].y1+””;
b1_coeff_9359.value = polys_9359[0].b+””;
x1_coeff_9359.value = polys_9359[0].x1+””;

p1_x_9359.value = polys_9359[0].p1.x+””;
p1_y_9359.value = polys_9359[0].p1.y+””;
p2_x_9359.value = polys_9359[0].p2.x+””;
p2_y_9359.value = polys_9359[0].p2.y+””;
}

//init_mouse();

var c_9359=document.getElementById(“myCanvas_9359”);
var ctx_9359=c_9359.getContext(“2d”);

var change = 0.0001;

function create_lines_9359 () {
//draw line
//document.write(“hello world! “);
var polys = [];
polys.push(addPoly(0,2, 3));
document.getElementById(‘testing’).innerHTML = “Hello”;
polys[0].set_2_points_line();
document.getElementById(‘testing’).innerHTML = “Hello4″;

// polys[1].color = ‘#8C8’;

return polys;
}

var polys_9359 = create_lines_9359();

var x1=xp(-10);
var y1=yp(1);
var x2=xp(10);
var y2=yp(1);
var dc_9359=0.05;

var t_9359 = 0;
var dt_9359 = 100;
//end_ct = 0;
var st_pt_x_9359 = 2;
var st_pt_y_9359 = 1;
var show_y_intercept_9359 = 1; //1 to show y intercept on startup
var show_intercepts_9359 = 0; // 1 to show the intercepts
var show_slope_9359 = 0; // 1 to show the slope
var show_2pts_9359 = 0; // 1 to show the two points from which line can be calculated

var move_dir_9359 = 1.0; // 1 for up

//document.getElementById(‘comment_spot’).innerHTML = polys_9359[0].a+” “+polys_9359[0].b+” “+polys_9359[0].c+” : “+polys_9359[0].h+” “+polys_9359[0].k+” “;

document.getElementById(‘testing’).innerHTML = “Hello3”;

//slope-intercept form
var b_coeff_9359 = document.getElementById(“b_coeff_9359”);
var c_coeff_9359 = document.getElementById(“c_coeff_9359”);

//point-slope form
var y1_coeff_9359 = document.getElementById(“y1_coeff_9359”);
var b1_coeff_9359 = document.getElementById(“b1_coeff_9359”);
var x1_coeff_9359 = document.getElementById(“x1_coeff_9359”);

//equation from two points
var p1_x_9359 = document.getElementById(“x1_9359”);
var p1_y_9359 = document.getElementById(“y1_9359”);
var p2_x_9359 = document.getElementById(“x2_9359”);
var p2_y_9359 = document.getElementById(“y2_9359”);

//options
var show_y_intercept_ctrl_9359 = document.getElementById(“show_y_intercept_9359”);
if (show_y_intercept_9359 == 0) {show_y_intercept_ctrl_9359.checked=false;
} else {show_y_intercept_ctrl_9359.checked=true;}

var show_intercepts_ctrl_9359 = document.getElementById(“show_intercepts_9359”);
if (show_intercepts_9359 == 0) {show_intercepts_ctrl_9359.checked=false;
} else {show_intercepts_ctrl_9359.checked=true;}

var show_slope_ctrl_9359 = document.getElementById(“show_slope_9359”);
if (show_slope_9359 == 0) {show_slope_ctrl_9359.checked=false;
} else {show_slope_ctrl_9359.checked=true;}

var show_2pts_ctrl_9359 = document.getElementById(“show_pts_9359”);
if (show_2pts_9359 == 0) {show_2pts_ctrl_9359.checked=false;
} else {show_2pts_ctrl_9359.checked=true;}

update_form_9359();

//document.write(“test= “+c_coeff_9359.value+” “+polys_9359[0].c);
setInterval(“draw_9359(ctx_9359, polys_9359)”, dt_9359);

b_coeff_9359.onchange = function() {
polys_9359[0].set_b(parseFloat(this.value));
polys_9359[0].update_point_slope_form_line();
polys_9359[0].set_2_points_line();
update_form_9359();
}
c_coeff_9359.onchange = function() {
//polys_9359[0].c = parseFloat(this.value);
polys_9359[0].set_c(parseFloat(this.value));
polys_9359[0].update_point_slope_form_line();
polys_9359[0].set_2_points_line();
update_form_9359();
}

y1_coeff_9359.onchange = function() {
//polys_9359[0].a = parseFloat(this.value);
polys_9359[0].y1 = parseFloat(this.value);
polys_9359[0].update_slope_intercept_form_line();
polys_9359[0].set_2_points_line();
update_form_9359();
}

b1_coeff_9359.onchange = function() {
polys_9359[0].set_b(parseFloat(this.value));
polys_9359[0].update_slope_intercept_form_line();
polys_9359[0].set_2_points_line();
update_form_9359();
}

x1_coeff_9359.onchange = function() {
polys_9359[0].x1 = parseFloat(this.value);
polys_9359[0].update_slope_intercept_form_line();
polys_9359[0].set_2_points_line();
polys_9359[0].set_order()
update_form_9359();
}

p1_x_9359.onchange = function() {
polys_9359[0].p1.x = parseFloat(this.value);
polys_9359[0].update_line_from_2pts();
polys_9359[0].set_order()
update_form_9359();
}

p2_x_9359.onchange = function() {
polys_9359[0].p2.x = parseFloat(this.value);
polys_9359[0].update_line_from_2pts();
polys_9359[0].set_order()
update_form_9359();
}

p1_y_9359.onchange = function() {
polys_9359[0].p1.y = parseFloat(this.value);
polys_9359[0].update_line_from_2pts();
polys_9359[0].set_order()
update_form_9359();
}

p2_y_9359.onchange = function() {
polys_9359[0].p2.y = parseFloat(this.value);
polys_9359[0].update_line_from_2pts();
polys_9359[0].set_order()
update_form_9359();
}

//draw_9359();
//document.write(“x”+x2+”x”);
//ctx_9359.fillText (“n=”, xp(5), yp(5));

[/script]

[/inline]

Curious Correlations

The Correlated website asks people different, apparently unrelated questions every day and mines the data for unexpected patterns.

In general, 72 percent of people are fans of the serial comma. But among those who prefer Tau as the circle constant over Pi, 90 percent are fans of the serial comma.

— ᔥ Correlated.org: March 23’s Correlation.

Two sets of data are said to be correlated when there is a relationship between them: the height of a fall is correlated to the number of bones broken; the temperature of the water is correlated to the amount of time the beaker sits on the hot plate (see here).

snow-T_data-0643 — A positive correlation between the time (x-axis) and the temperature (y-axis).

In fact, if we can come up with a line that matches the trend, we can figure out how good the trend is.

The first thing to try is usually a straight line, using a linear regression, which is pretty easy to do with Excel. I put the data from the graph above into Excel (melting-snow-experiment.xls) and plotted a linear regression for only the highlighted data points that seem to follow a nice, linear trend.

melting-snow-graph-2 — Correlation between temperature (y) and time (x) for the highlighted (red) data points.

You’ll notice on the top right corner of the graph two things: the equation of the line and the R², regression coefficient, that tells how good the correlation is.

The equation of the line is:

y = 4.4945 x – 23.65

which can be used to predict the temperature where the data-points are missing (y is the temperature and x is the time).

You’ll observe that the slope of the line is about 4.5 ºC/min. I had my students draw trendlines by hand, and they came up with slopes between 4.35 and 5, depending on the data points they used.

The regression coefficient tells how well your data line up. The better they line up the better the correlation. A perfect match, with all points on the line, will have a regression coefficient value of 1.0. Our regression coefficient is 0.9939, which is pretty good.

If we introduce a little random error to all the data points, we’d reduce the regression coefficient like this (where R² is now 0.831):

snow-melting-randomized — Adding in some random error causes the data to scatter more, making for a worse correlation. The black dots are the original data, while the red dots include some random error.

The correlation trend lines don’t just have to go up. Some things are negatively correlated — when one goes up the other goes down — such as the relationship between the number of hours spent watching TV and students’ grades.

negative-correlation — The negative correlation between grades and TV watching. Image: ᔥ Lanthier (2002).

Correlation versus Causation

However, just because two things are correlated does not mean that one causes the other.

A jar of water on a hot-plate will see its temperature rise with time because heat is transferred (via conduction) from the hot-plate to the water.

On the other hand, while it might seem reasonable that more TV might take time away from studying, resulting in poorer grades, it might be that students who score poorly are demoralized and so spend more time watching TV; what causes what is unclear — these two things might not be related at all.

Which brings us back to the Correlated.org website. They’re collecting a lot of seemingly random data and just trying to see what things match up.

Curiously, many scientists do this all the time — typically using a technique called multiple regression. Understandably, others are more than a little skeptical. The key problem is that people too easily leap from seeing a correlation to assuming that one thing causes the other.

Jupiter and Venus in Conjuction

jupiter-venus-0847 — Venus (brighter) and Jupiter.

Jupiter and Venus have been sitting near the western horizon, shining so brightly that even I have noticed them. Phil Plait explains with some back-of-the-envelope math, why Venus is brighter even though it’s smaller than Jupiter. It’s a nice example of how a little math can do a great job explaining how the world (and others) works.

Everything You (N)ever Wanted to Know About Parabolas

So that my students could more easily check their answers graphically, I put together a page with a more complete analysis of parabolas (click this link for more details).

[inline]

Analyzing Parabolas

Standard Form	Vertex Form
`y = a x² + b x + c`	`y = a (x – h)² + k`
y = x² + x +	y = ( x – ) ² +

Intercepts:	Vertex:
Focus:	Directrix:	Axis:

Solution by Factoring:

y = x² x

[script type=”text/javascript”]
var width=500;
var height=500;
var xrange=10;
var yrange=10;

mx = width/(2.0*xrange);
bx = width/2.0;
my = -height/(2.0*yrange);
by = height/2.0;

function draw_9239(ctx, polys) {
t_9239=t_9239+dt_9239;
//ctx.fillText (“t=”+t, xp(5), yp(5));
ctx.clearRect(0,0,width,height);

polys[0].drawAxes(ctx);
ctx.lineWidth=2;
polys[0].draw(ctx);

polys[0].write_eqn2(ctx);

//polys[0].y_intercepts(ctx);
//write intercepts on graph

// SHOW VERTEX
if (show_vertex_ctrl_9239.checked==true) {
polys[0].draw_vertex(ctx);
document.getElementById(‘vertex_pos_9239’).innerHTML = “(“+polys_9239[0].vertex.x.toPrecision(2)+ ” , “+polys_9239[0].vertex.y.toPrecision(2)+ ” )”;
} else { document.getElementById(‘vertex_pos_9239’).innerHTML = “”;}

// SHOW FOCUS
if (show_focus_ctrl_9239.checked==true) {
polys[0].draw_focus(ctx);
document.getElementById(‘focus_pos_9239’).innerHTML = “(“+polys_9239[0].focus.x.toPrecision(2)+ ” , “+polys_9239[0].focus.y.toPrecision(2)+ ” )”;
} else { document.getElementById(‘focus_pos_9239’).innerHTML = “”;}

// SHOW DIRECTRIX
if (show_directrix_ctrl_9239.checked==true) {
polys[0].draw_directrix(ctx);
document.getElementById(‘directrix_pos_9239’).innerHTML = polys[0].directrix.get_eqn2(“y”,”x”,”html”);

polys[0].directrix.write_eqn2(ctx, polys[0].directrix.get_eqn2(“directrix: y”));
} else { document.getElementById(‘directrix_pos_9239’).innerHTML = “”;}

// SHOW AXIS
if (show_axis_ctrl_9239.checked==true) {
polys[0].draw_parabola_axis(ctx);
document.getElementById(‘axis_pos_9239’).innerHTML = “x = “+polys[0].vertex.x.toPrecision(2);
}

//SHOW INTERCEPTS
ctx.textAlign=”center”;
if (show_intercepts_ctrl_9239.checked==true) {
polys[0].x_intercepts(ctx);
ctx.fillText (‘x intercepts: (when y=0)’, xp(6), yp(8));
//ctx.fillText (‘intercepts=’+polys[0].x_intcpts.length, xp(5), yp(-5));
if (polys[0].order == 2) {
if (polys[0].x_intcpts.length > 0) {
line = “0 = “;
for (var i=0; i 0.0) { sign=”-“;} else {sign=”+”;}
line = line + “(x “+sign+” “+ Math.abs(polys[0].x_intcpts[i].toPrecision(2))+ “)”;
}
ctx.fillText (line, xp(6), yp(7));
for (var i=0; i 0) {
for (var i=0; i2 “+polys[0].bsign+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;

solution = solution + ‘Factoring: ‘;

and solve for x:
‘;
for (var i=0; i‘;
}
document.getElementById(‘equation_9239’).innerHTML = solution;
}

else if (polys[0].order == 1) {
solution = solution + ‘
‘;
solution = solution + “y = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;
solution = solution + ‘

Set y=0 and solve for x:
‘;
solution = solution + ” 0 = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;
solution = solution + ‘ ‘;
solution = solution + (-1.0*polys[0].c).toPrecision(2) +” = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+”

“;
solution = solution + ‘ ‘;
solution = solution + (-1.0*polys[0].c).toPrecision(2)+”/”+polys[0].b.toPrecision(2)+” = “+” x “+”

“;
solution = solution + ‘ ‘;
solution = solution + “x = “+ (-1.0*polys[0].c/polys[0].b).toPrecision(4)+”

“;

document.getElementById(‘equation_9239’).innerHTML = solution;
}

}

function update_form_9239 () {
a_coeff_9239.value = polys_9239[0].a+””;
b_coeff_9239.value = polys_9239[0].b+””;
c_coeff_9239.value = polys_9239[0].c+””;

av_coeff_9239.value = polys_9239[0].a+””;
hv_coeff_9239.value = polys_9239[0].h+””;
kv_coeff_9239.value = polys_9239[0].k+””;

}

//init_mouse();

var c_9239=document.getElementById(“myCanvas_9239”);
var ctx_9239=c_9239.getContext(“2d”);

var change = 0.0001;

function create_lines_9239 () {
//draw line
//document.write(“hello world! “);
var polys = [];
polys.push(addPoly(1,6, 5));

// polys.push(addPoly(0.25, 1, 0));
// polys[1].color = ‘#8C8’;

return polys;
}

var polys_9239 = create_lines_9239();

var x1=xp(-10);
var y1=yp(1);
var x2=xp(10);
var y2=yp(1);
var dc_9239=0.05;

var t_9239 = 0;
var dt_9239 = 100;
//end_ct = 0;
var st_pt_x_9239 = 2;
var st_pt_y_9239 = 1;
var show_vertex_9239 = 1; //1 to show vertex on startup
var show_focus_9239 = 1; // 1 to show the focus
var show_intercepts_9239 = 1; // 1 to show the intercepts
var show_directrix_9239 = 1; // 1 to show the directrix
var show_axis_9239 = 1; //1 to show the axis of the parabola

var move_dir_9239 = 1.0; // 1 for up

//document.getElementById(‘comment_spot’).innerHTML = polys_9239[0].a+” “+polys_9239[0].b+” “+polys_9239[0].c+” : “+polys_9239[0].h+” “+polys_9239[0].k+” “;

//standard form
var a_coeff_9239 = document.getElementById(“a_coeff_9239”);
var b_coeff_9239 = document.getElementById(“b_coeff_9239”);
var c_coeff_9239 = document.getElementById(“c_coeff_9239”);

//vertex form
var av_coeff_9239 = document.getElementById(“av_coeff_9239”);
var hv_coeff_9239 = document.getElementById(“hv_coeff_9239”);
var kv_coeff_9239 = document.getElementById(“kv_coeff_9239”);

//options
var show_vertex_ctrl_9239 = document.getElementById(“show_vertex_9239”);
if (show_vertex_9239 == 0) {show_vertex_ctrl_9239.checked=false;
} else {show_vertex_ctrl_9239.checked=true;}

var show_focus_ctrl_9239 = document.getElementById(“show_focus_9239”);
if (show_focus_9239 == 0) {show_focus_ctrl_9239.checked=false;
} else {show_focus_ctrl_9239.checked=true;}

var show_intercepts_ctrl_9239 = document.getElementById(“show_intercepts_9239”);
if (show_intercepts_9239 == 0) {show_intercepts_ctrl_9239.checked=false;
} else {show_intercepts_ctrl_9239.checked=true;}

var show_directrix_ctrl_9239 = document.getElementById(“show_directrix_9239”);
if (show_directrix_9239 == 0) {show_directrix_ctrl_9239.checked=false;
} else {show_directrix_ctrl_9239.checked=true;}

var show_axis_ctrl_9239 = document.getElementById(“show_axis_9239”);
if (show_axis_9239 == 0) {show_axis_ctrl_9239.checked=false;
} else {show_axis_ctrl_9239.checked=true;}

update_form_9239();

//document.write(“test= “+c_coeff_9239.value+” “+polys_9239[0].c);
setInterval(“draw_9239(ctx_9239, polys_9239)”, dt_9239);

a_coeff_9239.onchange = function() {
//polys_9239[0].a = parseFloat(this.value);
polys_9239[0].set_a(parseFloat(this.value));
polys_9239[0].update_vertex_form_parabola();
update_form_9239();
}
b_coeff_9239.onchange = function() {
//polys_9239[0].b = parseFloat(this.value);
polys_9239[0].set_b(parseFloat(this.value));
polys_9239[0].update_vertex_form_parabola();
update_form_9239();
}
c_coeff_9239.onchange = function() {
//polys_9239[0].c = parseFloat(this.value);
polys_9239[0].set_c(parseFloat(this.value));
polys_9239[0].update_vertex_form_parabola();
update_form_9239();
}

av_coeff_9239.onchange = function() {
//polys_9239[0].a = parseFloat(this.value);
polys_9239[0].set_a(parseFloat(this.value));
polys_9239[0].update_standard_form_parabola();
update_form_9239();
}

hv_coeff_9239.onchange = function() {
polys_9239[0].h = parseFloat(this.value);
polys_9239[0].update_standard_form_parabola();
polys_9239[0].set_order()
update_form_9239();
}

kv_coeff_9239.onchange = function() {
polys_9239[0].k = parseFloat(this.value);
polys_9239[0].update_standard_form_parabola();
polys_9239[0].set_order()
update_form_9239();
}

//draw_9239();
//document.write(“x”+x2+”x”);
//ctx_9239.fillText (“n=”, xp(5), yp(5));

[/script]

[/inline]

Converting the forms

The key relationships are the ones to convert from the standard form of the parabolic equation:

$y = a x^2 + b x + c$

(1)

to the vertex form:

$y = a (x - h)^2 + k$

(2)

If you multiply out the vertex equation form you get:

y = a x² – 2ah x + ah² + k

(3)

When you compare this equation to the standard form of the equation (Equation 1), if you look at the coefficients and the constants, you can see that:

To convert from the vertex to the standard form use:

         $a = a$ (4)

         $b = -2ah$ (5)

         $c = ah^2 + k$ (6)

Going the other way,

To convert from the standard to the vertex form of parabolic equations use:

         $a = a$
(7)

         $h = \frac{-b}{2a}$
(8)

         $k = c - ah^2$
(9)

Although it is sometimes convenient to let k not depend on coefficients from its own equation:

$k = c - \frac{b^2}{4a}$ (10)

The Vertex and the Axis

The nice thing about the vertex form of the equation of the parabola is that if you want the find the coordinates of the vertex of the parabola, they’re right there in the equation.

Specifically, the vertex is located at the point:

$(x_v, y_v) = (h, k)$

(11)

The axis of the parabola is the vertical line going through the vertex, so:

The equation for the axis of a parabola is:

$x = h$

(12)

Focus and Directrix

Finally, it’s important to note that the distance (d) from the vertex of the parabola to its focus is given by:

$d = \frac{1}{4a}$

(13)

Which you can just add d on to the coordinates of the vertex (Equation 11) to get the location of the focus.

$(x_f, y_f) = (x_v, y_v + d)$

(14)

The directrix is just the opposite, vertical distance away, so the equation for the directrix is the equation of the horizontal line at:

$y = y_v + d$

(15)

References

There are already some excellent parabola references out there including:

Wonderful interactive graphs by Murray Bourne.
Nice simple explanations of the different forms of the equations.
More complex explanations from Wolfram Alpha.

Euler’s Method for Approximating a Solution to a Differential Equation

Based on Euler’s Method, this interactive graph illustrates a numerical method for solving differential equations. This approach is at the core of many sophisticated computer models of physical phenomena (like climate and weather).

[inline]

Starting point: (x,y) = ( , )
Step size:
Direction:

Slope equation: dy/dx = x +
Show analytical solution:

If you know the equation for the slope of a curve (the red line for example),

and a point that the curve passes through, such as , you can integrate to find the equation of the curve:

[script type=”text/javascript”]

var width=500;
var height=500;
var xrange=10;
var yrange=10;

mx = width/(2.0*xrange);
bx = width/2.0;
my = -height/(2.0*yrange);
by = height/2.0;

function upause () {
ct = 1;
}

function draw_9110(ctx, polys) {
t_9110=t_9110+dt_9110;
//ctx.fillText (“t=”+t, xp(5), yp(5));
ctx.clearRect(0,0,width,height);

polys[0].drawAxes(ctx);
polys[0].slopeField(ctx, 1.0, 1.0, 0.5);
ctx.lineWidth=2;
polys[0].draw(ctx);
polys[0].write_eqn(ctx, “slope = dy/dx”);

eu = eu_9110;
//override nsteps values
//max_nsteps_9110 = eu.nsteps;
//eu.nsteps = nsteps_9110;

if (nsteps_9110 <= max_nsteps_9110) { nsteps_9110 = nsteps_9110 + 1;} else { nsteps_9110 = 0; } eu.nsteps = nsteps_9110; if (show_parabola_9110 == 1) { polys[0].Integrate(ctx, eu.x1, eu.y1); polys[0].integral.color = '#3c3'; polys[0].integral.draw(ctx); } pos = polys[0].EulerApprox(ctx, eu); //document.getElementById('comment_9110').innerHTML = eu.nsteps+ " " + eu.x1 + " " + eu.y1+ " " + eu.dx+ " " + eu.dir+ " " + max_nsteps_9110; //starting point label ctx.textAlign="right"; ctx.textBaseline="alphabetic"; ctx.font = "14pt Calibri"; ctx.fillStyle = "#00f"; ctx.fillText ('start = ('+eu.x1+','+eu.y1+")", xp(eu.x1-0.25), yp(eu.y1-0.5)); //pos = polys[0].EulerApprox(ctx, st_pt_x_9110, st_pt_y_9110, 0.5,20,-1); //pos = polys[0].EulerApprox(ctx, st_pt_x_9110, st_pt_y_9110, 1, 6,1); //draw starting point ctx.strokeStyle="#00f"; ctx.lineWidth=2; ctx.beginPath(); ctx.arc(xp(eu.x1),yp(eu.y1),dxp(0.1),0,Math.PI*2); ctx.closePath(); ctx.stroke(); //ctx.fillText (' c='+move_dir_9110+' '+polys[1].c, xp(5), yp(5)); } //init_mouse(); var c_9110=document.getElementById("myCanvas_9110"); var ctx_9110=c_9110.getContext("2d"); var change = 0.0001; function create_lines_9110 () { //draw line var polys = []; polys.push(addPoly(0, 0.5, -1)); return polys; } function set_max_nsteps_9110 (eu) { max_nsteps_9110 = 1.5*(xrange - eu.x1)/eu.dx; } var polys_9110 = create_lines_9110(); var x1=xp(-10); var y1=yp(1); var x2=xp(10); var y2=yp(1); var dc_9110=0.05; var t_9110 = 0; var dt_9110 = 500; var st_dx_9110 = 1.0; var st_nsteps_9110 = 0; var nsteps_9110 = 0; var max_nsteps_9110 = 20; var dir_9110 = 1; var show_parabola_9110 = 1; var st_pt_x_9110 = -2; var st_pt_y_9110 = -3; var move_dir_9110 = 1.0; // 1 for up //Form interaction function update_form_9110 (x, y, dx, nsteps, dir, b, c, show_para) { x_9110.value = st_pt_x_9110+""; y_9110.value = st_pt_y_9110+""; dx_9110.value = st_dx_9110.toPrecision(2); //c_max_nsteps_9110.value = max_nsteps_9110+""; //document.getElementById('comment_9110').innerHTML = c_dir_9110; if (dir == 1) { c_dir_9110.selectedIndex = 0; } else {c_dir_9110.selectedIndex = 1;} b_9110.value = b+""; c_9110.value = c+""; if (show_para == 1) { ctrl_show.checked = 1; } else {ctrl_show.checked = 0;} } function get_euler_form_9110 () { pos = {x : parseFloat(x_9110.value), y : parseFloat(y_9110.value)} if (c_dir_9110.selectedIndex == 0) { dir = 1;} else {dir = -1;} eu = addEuler(pos.x, pos.y, parseFloat(dx_9110.value), max_nsteps_9110, dir); return eu } function update_solution_9110 (ctx, eu) { //update equations and solution document.getElementById('slope_eqn_9110').innerHTML = polys_9110[0].get_eqn("dy/dx"); //document.getElementById('eqn_9110').innerHTML = "hey"+eu.y1; polys_9110[0].Integrate(ctx, eu.x1, eu.y1); document.getElementById('eqn_9110').innerHTML = polys_9110[0].integral.get_eqn(); document.getElementById('init_pt_9110').innerHTML = "("+eu.x1+","+eu.y1+")"; } function add_euler_line() { eu_9110 = get_euler_form_9110 (); max_nsteps_9110 = eu_9110.nsteps; nsteps_9110 = 0; } var x_9110 = document.getElementById("x_9110"); var y_9110 = document.getElementById("y_9110"); var dx_9110 = document.getElementById("dx_9110"); //var c_max_nsteps_9110 = document.getElementById("nsteps_9110"); var c_dir_9110 = document.getElementById("dir_9110"); var b_9110 = document.getElementById("b_9110"); var c_9110 = document.getElementById("c_9110"); var ctrl_show = document.getElementById("chk_show_para_9110"); update_form_9110(x_9110, y_9110, dx_9110, nsteps_9110, dir_9110, polys_9110[0].b, polys_9110[0].c, show_parabola_9110); var eu_9110 = get_euler_form_9110 (); set_max_nsteps_9110(eu_9110); update_solution_9110(ctx_9110, eu_9110); setInterval("draw_9110(ctx_9110, polys_9110)", dt_9110); x_9110.onchange = function() { eu_9110 = get_euler_form_9110 (); max_nsteps_9110 = eu_9110.nsteps; nsteps_9110 = 0; } y_9110.onchange = function() { eu_9110 = get_euler_form_9110 (); max_nsteps_9110 = eu_9110.nsteps; nsteps_9110 = 0; } c_dir_9110.onchange = function() { eu_9110 = get_euler_form_9110 (); max_nsteps_9110 = eu_9110.nsteps; nsteps_9110 = 0; } dx_9110.onchange = function() { eu_9110 = get_euler_form_9110 (); max_nsteps_9110 = eu_9110.nsteps; //max_nsteps_9110 = 1.4 * (10 - eu_9110.x1)/eu_9110.dx; set_max_nsteps_9110(eu_9110); nsteps_9110 = 0; } b_9110.onchange = function() { polys_9110[0].set_b(parseFloat(this.value)); eu_9110 = get_euler_form_9110 (); max_nsteps_9110 = eu_9110.nsteps; nsteps_9110 = 0; } c_9110.onchange = function() { polys_9110[0].set_c(parseFloat(this.value)); eu_9110 = get_euler_form_9110 (); max_nsteps_9110 = eu_9110.nsteps; nsteps_9110 = 0; } ctrl_show.onchange = function() { if (this.checked == 1) { show_parabola_9110 = 1;} else {show_parabola_9110 = 0} } [/script] [/inline]

If you don’t have a starting point (initial condition), you can draw a slope field to see what the general pattern of all the possible solutions.

Even with a starting point, however, there are just times when you can’t integrate the slope equation — it’s either too difficult or even impossible.

Then, what you can do is come up with an approximation of what the curve looks like by projecting along the slope from the starting point.

The program above demonstrates how it’s done. This approach is called Euler’s Method, and is gives a numerical approximation rather than finding the exact, analytical solution using calculus (integration).

So why use an approximation when you can find the exact solution? Because, there are quite a number of problems that are impossible or extremely difficult to solve analytically, things like: the diffusion of pollution in a lake; how changing temperature in the atmosphere gives you weather and climate; the flow of groundwater in aquifers; stresses on structural members of buildings; and the list goes on and on.

As with most types of numerical approximations, you get better results if you can reduce the step size between projections of the slope. Try changing the numbers and see.

A more detailed version, with solutions, is here: Euler’s Method.

A good reference: Euler’s Method by Paul Dawkins.

Slope Fields

[inline]

[script type=”text/javascript”]
var width=500;
var height=500;
var xrange=10;
var yrange=10;

mx = width/(2.0*xrange);
bx = width/2.0;
my = -height/(2.0*yrange);
by = height/2.0;

function draw9083(ctx, polys) {
t=t+dt;
//ctx.fillText (“t=”+t, xp(5), yp(5));
ctx.clearRect(0,0,width,height);

polys[0].drawAxes(ctx);
polys[0].slopeField(ctx, 1.0, 1.0, 0.5);
ctx.lineWidth=2;
polys[0].draw(ctx);
polys[0].write_eqn(ctx, “dy/dx “);

}

//init_mouse();

var c9083=document.getElementById(“myCanvas9083”);
var ctx9083=c9083.getContext(“2d”);

var change = 0.0001;

function create_lines9083 () {
//draw line
//document.write(“hello world! “);
var polys = [];
polys.push(addPoly(0, 0.5, 1));

return polys;
}

var polys9083 = create_lines9083();

var x1=xp(-10);
var y1=yp(1);
var x2=xp(10);
var y2=yp(1);
var dy=0.01;

var t = 0;
var dt = 50;
end_ct = 0;

var move_dir = 1; // 1 for up

//draw9083();
//document.write(“x”+x2+”x”);
//ctx9083.fillText (“n=”, xp(5), yp(5));
setInterval(“draw9083(ctx9083, polys9083)”, dt);

[/script]
[/inline]

Say you have the equation that gives you the slope of a curve (let $\frac{dy}{dx}$ ) be the slope):
$! \frac{dy}{dx} = \frac{1}{2} x + 1$

When you use integration to solve the equation, there are quite the number of possible solutions (infinite actually), because when you integrate:

$! y = \int (\frac{1}{2} x + 1 ) dx$

you get:
$! y = \frac{1}{4} x^2 + x + c$

where c is a constant. Unfortunately, you don’t know what c is without more information; it could be anything.

However, even without integrating, we can get a feel for what the curve will look like by plotting what the slope will look like at a bunch of different points in space. This comes in really handy when you end up with a equation for slope that is really hard — or even impossible — to solve.

The graph below show a curve of possible solutions to the slope equation. You should be able to see, as the graph slowly moves up and down, how the slope of the graph corresponds to the slope field.

[inline]

[script type=”text/javascript”]
var width=500;
var height=500;
var xrange=10;
var yrange=10;

mx = width/(2.0*xrange);
bx = width/2.0;
my = -height/(2.0*yrange);
by = height/2.0;

function draw9083b(ctx, polys) {
t9083b=t9083b+dt9083b;
//ctx.fillText (“t=”+t, xp(5), yp(5));
ctx.clearRect(0,0,width,height);

polys[0].drawAxes(ctx);
polys[0].slopeField(ctx, 1.0, 1.0, 0.5);
ctx.lineWidth=2;
polys[0].draw(ctx);
polys[0].write_eqn(ctx, “dy/dx “);

if (polys[1].c > yrange) {
move_dir9083b = -1.0;
polys[1].c = yrange;
}
else if (polys[1].c < -yrange) { move_dir9083b = 1.0; polys[1].c = -yrange; } polys[1].c = polys[1].c + dc9083b*move_dir9083b; polys[1].draw(ctx); polys[1].write_eqn(ctx); //ctx.fillText (' c='+move_dir9083b+' '+polys[1].c, xp(5), yp(5)); } //init_mouse(); var c9083b=document.getElementById("myCanvas9083b"); var ctx9083b=c9083b.getContext("2d"); var change = 0.0001; function create_lines9083b () { //draw line //document.write("hello world! "); var polys = []; polys.push(addPoly(0, 0.5, 1)); polys.push(addPoly(0.25, 1, 0)); polys[1].color = '#8C8'; return polys; } var polys9083b = create_lines9083b(); var x1=xp(-10); var y1=yp(1); var x2=xp(10); var y2=yp(1); var dc9083b=0.05; var t9083b = 0; var dt9083b = 100; //end_ct = 0; var move_dir9083b = 1.0; // 1 for up //draw9083b(); //document.write("x"+x2+"x"); //ctx9083b.fillText ("n=", xp(5), yp(5)); setInterval("draw9083b(ctx9083b, polys9083b)", dt9083b); [/script] [/inline]

Straight Lines

[inline]

[script type=”text/javascript”]
var width=500;
var height=500;
var xrange=10;
var yrange=10;

mx = width/(2.0*xrange);
bx = width/2.0;
my = -height/(2.0*yrange);
by = height/2.0;

function draw8587(ctx, polys) {
t=t+dt;
//ctx.fillText (“t=”+t, xp(5), yp(5));
ctx.clearRect(0,0,width,height);

polys[0].drawAxes(ctx);
//drawAxes(ctx);
ctx.lineWidth=3;
//ctx.beginPath();
//ctx.moveTo(x1,y1);
//ctx.lineTo(x2,y2);
//ctx.stroke();
//ctx.closePath();
//y2+=dyp(dy);

// add polynomial timing
// First move (from y=0 to y=1)
if (polys[0].c < 1.0) { polys[0].c = polys[0].c + 2.0*dt*change*move_dir; } // Second move (change from y=1 to y=0.5x+1) else if (polys[0].b < 0.5) { polys[0].b = polys[0].b + dt*change*move_dir; polys[0].order = 1; } // Third move (change from y=0.5x+1 to y=0.5x+4) else if (polys[0].c < 4.0) { polys[0].c = polys[0].c + 2.*dt*change*move_dir; //polys[0].order = 1; } else { //move_dir = move_dir * -1; end_ct = end_ct + dt; if (end_ct >= dt*40) {
polys[0].a = 0;
polys[0].b = 0;
polys[0].c = 0;
polys[0].order = 0;
}
}
ctx.textAlign=”center”;
ctx.textBaseline=”alphabetic”;
ctx.font = “14pt Arial”;
ctx.fillStyle = ‘#f00’;
ctx.fillText (“Equation of a Line”, xp(-5), yp(9));
ctx.fillText (“y = mx + b”, xp(-5), yp(5));
ctx.font = “12pt Arial”;
//ctx.fillText (“y = “+polys[0].b.toPrecision(1)+”x + “+ polys[0].c.toPrecision(2), xp(-5), yp(7));
ctx.fillText (“b = intercept = “+polys[0].c.toPrecision(2), xp(-7), yp(3));

//draw polynomials
ctx.lineWidth=3;
for (var i=0; i

Here’s a prototype for showing how the equation of a straight line changes as you change its slope (m) and intercept (b):
$! y = mx + b$

It starts with an horizontal line along the x-axis, where the slope is zero and the intercept is zero:
$! y = 0.0$

The line moves upward, but stays horizontal, until the intercept is 1.0:
$! y = 1.0$

The slope increases from horizontal (m = 0), gradually, until the slope is 0.5:
$! y = 0.5x + 1.0$

Finally, we move the line upwards again, without changing the slope (m = 0.5), until the intercept is equal to 4.0:
$! y = 0.5x + 4.0$

Now I just need to figure out how to make them interactive.