If you recall, straight lines have a general equation that looks like this:
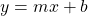 (1)
(1)
This is called the slope-intercept form of the equation, because m gives the slope, and b tells where the line intercepts the y-axis. For example the line:
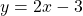 (2)
(2)
looks like:
Now, in the slope-intercept form, m and b represent numbers. In our example, m = 2 and b = 3.
So what if, instead of calling them m and b we used the same letter (let’s use a) and just gave two different subscripts so:
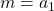 and,
and,
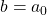
therefore equation (1):
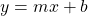
becomes:
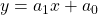 (3)
(3)
Now, in case you’re wondering why we picked m = a1 instead of m = a0, it’s because of the exponents of x. You see, in the equation x has an exponent of 1, and the constant b could be thought to be multiplying x with an exponent of 0. Considering this, we could rewrite our equation of the line (2):
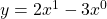 (4)
(4)
since:
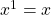 and,
and,
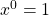
we get:
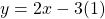
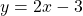
So in equation (3) the subscript refers to the exponent of x.
Now we can expand this a bit more. What if we had a term with x2 in an equation:
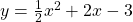 (5)
(5)
Now we have three coefficients:
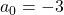 ,
,
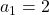 and,
and,
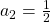 ,
,
And the graph would look like this.
Because of the x2 term (specifically because it has the highest exponent in the equation), this is called a second-order polynomial — that’s why the graph above has a little input box where the order is 2. In fact, on the graph above, you can change the order to see how the equation changes. Indeed, you can also change the coefficients to see how the graph changes.
A second order polynomial is a parabola, while, as you’ve probably guessed, a first order polynomial is a straight line. What’s a zero’th order polynomial?
Finally, we can write a general equation for a polynomial — just like we have the slope-intercept form of a line — using the a coefficients like:
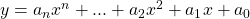
You can use the graphs to tinker around and see what different order polynomials look like, and how changing the coefficients change the graphs. I sort-of like the one below:
References
WolframAlpha has more details on polynomials.
The embedded graphs come from my own Polynomial Grapher.