Category: Natural World

Coon Creek Matrix Under the Microscope

Hunting for microscopic fossils at the dinner table. Inside the circle is 100x magnification; outside the circle the magnification is 1.

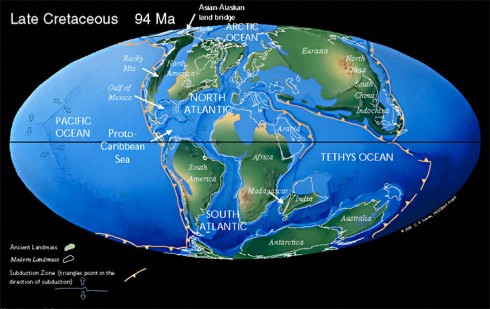
My students will tell you that I’m never happier than when I have my cup of tea. On the night after our visit to Coon Creek, I put a tiny sample, about the size of a matchstick’s head, of sediment matrix on a microscope slide, and added a drop of water to disperse the grains. Then I sat there, while the chaos of dinner-making swirled around me, and searched for tiny, microscopic fossils of creatures that died long ago. With my cup of hot tea beside me, it was like sitting in the eye of a storm, flaming hamburgers be damned, a modicum of sanity in the asylum.

Quartz grains from Coon Creek Formation sediment seen under the microscope at 100x magnification. Quartz is easy to identify because of the way it breaks with curved fractures.

The first thing I noticed though were the quartz grains. They’re very small, silt-sized, but are the largest grains in the sediment. They’re pretty easy to identify because they break like glass, with curved, conchoidal fractures. They’re also pretty little things under the microscope; little, sharp-peaked, transparent mountains.

Other minerals are visible in the sediments. Though they're relatively large they're still dwarfed by the quartz (100x magnification).

Other minerals are visible in the slides, but they’re dwarfed in size and quantity by the quartz. Yet there is enough of the dark green, glauconite clay to bind the quartz grains together and protect the shells embedded in the sediment from dissolution by the universal solvent, water.

It’s interesting to observe these other minerals, because they take the more classic crystalline shapes and forms. The sharp edges are parallel to one another because of the alignment of the atoms in the mineral crystal.

Snail like shape of what's probably a planktonic (lives in the water) foram. (100x magnification).

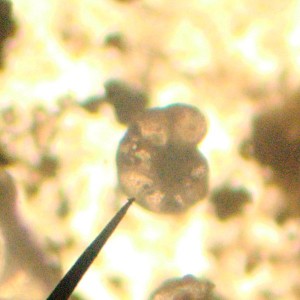
Finding the micro-fossils took a little patience. The entire slide had only four obvious specimens. Since they’re so small that meant a lot of going back and forth under the small field of view of the 100 magnification objective lens. They look like foraminfera to me, but it’s been a while since I’ve encountered them. Foraminfera, or forams for short, are tiny organisms that secrete beautiful calcium carbonate shells. They can be found in, or in the sediments beneath, most of the world’s oceans, particularly in the warmer areas.

Finding forams in the Coon Creek Matrix is a nice little exercise. One of my students, seeing what I was doing, wanted to try it too, so she made her own slide and searched until she found her own specimen. It was somewhat inspiring, so I’ve put together a more detailed post about finding microfossils.

We also found a neat little shell that looks like the overlapping scales on a pine cone. We were disconnected from the internet, so I was only able to look it up when I got back to school.

What looks like a type of boliviana foraminfera. It's benthic, which means that it lives in the sediments not in the water.
What looks like a type of bolivina foraminfera. It's benthic, which means that it lives in the sediments not in the water. (100x magnification).

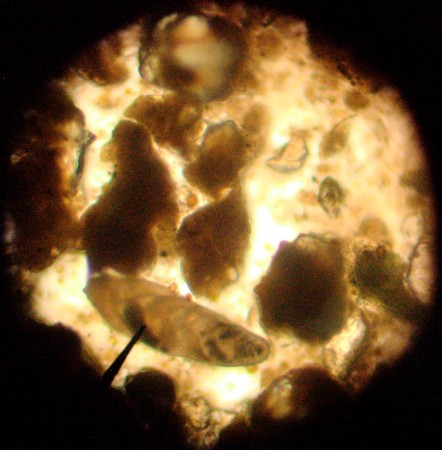
Dr. J Bret Bennington at Hofstra has posted a nice PowerPoint of his introduction to marine microfossils lecture. As a basic introduction, it’s quite comprehensible to middle-school students, or people like myself who did not pay as much attention as they should have during that part of Paleontology. Anyway, based on these notes, the pine-cone-shaped thing is probably a variety of bolivina, a benthic foraminfera. The Foraminifera.eu-Project, is a wonderful, volunteer-produced resource for pictures and identifying forams.

Bolivina are benthic, which means they spend most, if not all of their time in the mud. Planktonic micro-organisms, on the other hand, spend their lives floating around in the water.

Foraminfera have calcium carbonate shells, as do clams and oysters. In the shallow oceans there is a slow rain of them that cover the sea-bed over the millenia. You can end up with thick layers. In fact, the white cliffs of Dover are white because of all the microscopic calcium carbonate shells. In the deeper reaches of the oceans there are much fewer of these shells because they dissolve under high pressure. As a result, down there you tend to find microfossils of diatoms and radiolarians, things with silica shells. Silica is that same material from which glass is made, and is the same material in quartz.

Finding microfossils has actually been quite important for understanding the history of the Earth’s oceans and climate. But that’s another story.

Coon Creek Science Center: Collecting Cretaceous Fossils

70 million year old shell and its imprint in a clay matrix, collected at the Coon Creek Science Center.

Collecting the amazingly well-preserved Cretaceous molluscs and arthropods at the Coon Creek Science Center was an excellent way to learn about fossils and the geology of the Mississippi Embayment.

Consider: the actual shell of an actual organism that actually lived 70 million years ago; not the form of the shell, petrified in silica; not the silent imprint of ridges and grooves in the mud of some bivalve’s test, long dissolved by the silent flux of millenia of groundwater flow, although you can find those, too; but to stand in the daylight, on the gravel bar of a creek, and hold the actual shell of an actual marine organism that lived here when it was six meters under water.

When we got to Coon Creek, Pat Broadbent did her typical, excellent presentation, starting with the very basics question of, “What are fossils?” Apart from the aforementioned actual preserved shells, you can also find trace fossils, like, for example, where the imprints of the an organism is left in the mud while the shell itself has long dissolved away. They can be imprints, or molds of the shells. One of my students found the mold of a crab’s claw along the creek bed; the mud filling in the claw had solidified into rock but you could clearly see where the pincer once articulated.

Pat also talked about the Mississippi Embayment, which is the long, broad valley through which the Mississippi River flows.

The breakup of the supercontinent, Pangea. Notice how the North Atlantic Ocean is opening as North America pulls away from Europe and Africa. You can also see the flooded Mississippi Embayment. (Image from Scotese, C.R., 2002, http://www.scotese.com, (PALEOMAP website)).

When the supercontinent Pangea started to break up, North America pulled away from Europe and Africa. This created a rift that eventually became the North Atlantic Ocean. At about the same time, North America tried to split into two as a second rift was created, right where the Mississippi Embayment is today.

How the coastline of North America, has changed over the last 100 million years. The sediments at Coon Creek were deposited in the Cretaceous (black line). The current coastline is shown in blue. (Image from Wikipedia).

But the rift failed (Cox and Van Arsdale, 2007). It did, however, stretch and thin the continental crust enough to create a large inland sea running up the middle of North America. Over the 100 million years since, the rift formed, the Mississippi Embayment has filled in, first with oceanic sediment, but then with terrestrial sands and silts as the mountains to the east and west were eroded away and washed into the inland sea.

The layer of silt and glauconite clay that encases the fossils at Coon Creek is called the Coon Creek Formation. Pat was very clear that we should refer to this material surrounding the fossils as “matrix”. The “d” word was prohibited. These sediments were deposited while the sea still flooded the embayment. They formed a sand bank, several kilometers offshore.

I vaguely remember doing some research on glauconite a long time ago. Glauconite pellets are found in shallow marine waters, usually far enough away from the coastline so that sediment is deposited slowly, and it’s the finer materials, such as silts and clays, that are deposited. The water also needs to be deep enough to protect the fine sediment from the force of the waves. These are ideal conditions for clams, mussels, conchs, and their Cretaceous relatives.

A simple smear of the sediment across a microscope slide is enough to show that the matrix is has a lot of quartz. You need a microscope because the mineral grains are tiny, silt sized or smaller.

But the best part of looking at the slides is finding the microscopic fossils. They’re not as ubiquitous as you might think, but they’re there if you look. I found a couple of forams, a snail-like one and another that looks like a bolivina species.

What looks like a type of boliviana foraminfera. It's benthic, which means that it lives in the sediments not in the water.
What looks like a type of bolivina foraminfera. It's benthic, which means that it lives in the sediments not in the water. It is surrounded by silt-sized grains of quartz.

However, the smear slides came later. After Pat’s talk, she took us out to a small mound of matrix that had been excavated for sampling. Everyone grabbed chunks of matrix and pared away at them until they found something promising. These promising samples were wrapped in aluminum foil so we could clean them up under more controlled conditions.

Cleaning samples.

Cleaning takes time and patience, so Pat showed us how to do it, and each student worked on a single sample. The main idea is to create a display of the fossil using the matrix as a base. The general procedure is to:

  • Use a small pick, paintbrush and spray-bottle of water, to wash and wipe away the matrix from the fossil.
  • Let it dry out well, which usually takes about five days.
  • Paint the entire thing with a 50-50 mix of acrylic floor wax and water. Pat recommends Future Floor Wax, but that seems to have been rebranded out of existance.
  • Repeat that last step three times (let it dry for about 15 minutes inbetween) to get a well preserved, robust sample.

After the instructions on cleaning, we broke for lunch. For most of us lunch could not have come early enough, not because we were particularly hungry, but because it was quite cold outside. Just the week before the temperature had been above 20 °C, t-shirt weather. Now students were clustering around a couple space heaters trying to ward off frostbite (or at least that’s what they claimed). I did offer that they could stay inside after lunch while the rest of the class walked along the creek, but no-one took me up on it. I don’t know if it’s specific to this group or just to adolescents in general, but if there a chance to walk through water, and get dirty and wet, they’ll take it no matter what the consequence.

Students looking for fossils in gravel bar.

Walking the creek, pulling shells and molds out of the gravel bars, was the best part of the visit.

Students standing in the creek, testing their rubber boots.

The water was shallow, not getting up above the shins, despite the rain showers of the preceding days. A few students borrowed rubber boots, which half of them proceeded to fill with water.

There were quite a lot of fossils. Some of the bivalves have really thick strong shells that not only survived the 70 million years since the Cretaceous, but being washed out of the matrix and tumbled down a stream bed with all sorts of sand and gravel. Some of the casts, like the aforementioned arthropod claw, are also pretty robust.

Snail shell that's been in the ground for millions of years and then got washed out into a gravel bar.

A couple of the more interesting finds are the rather elongate tube like structures that are believed to be either fossilized burrows, or fish feces (coporolite). The material in the coporolite has been replaced by minerals, which is why it survived, but it still retains a little of the ick factor.

There’s an awful lot to learn at Coon Creek. I did not even mention the mesosaur skeletons that have been found there, but there is a nice IMAX movie, Sea Monsters, that’s a nice complement to the field trip because it’s set at the same time, and in the same marine environment as the Coon Creek Formation.

Drilling Through to the Mantle

Between 6 and 25 km thick, the Earth’s crust is an excruciatingly thin skin on a 6400 km globe. Yet even drilling to the bottom of the crust would require a remarkable feat of engineering. Some geologists want to try.

NPR’s Science Friday interviews Damon Teagle, one of the architects of the project. They want to drill in the ocean because oceanic crust is thinner than continental crust (on the other hand, it’s denser too, which is why it subducts).

Using different types of chocolate covered candy, they also have this wonderful video of the basalts, sheeted dykes and gabbros that make up the crust.

Coon Creek Immersion: Visiting the Cretaceous

70 million year old shell and its imprint collected at the Coon Creek Science Center.

Just got back from our immersion trip to collect Cretaceous fossils at the Coon Creek Science Center, and hiking in Natchez Trace State Park.

It was an excellent trip. Despite the cold, Pat Broadbent did her usual, excellent job explaining the geology of Coon Creek and showing us how to collect and preserve some wonderful specimens. Back at the cabins, we looked at some of the microfossils from the Coon Creek sediments (and some other microscopic crystals); similar fossils can tell us a lot about the Earth’s past climate.

Back at the Park, we traced a streamline from the watershed divide to its marshy estuary, and cooked an excellent seafood dinner as we learned about the major organ systems.

Dinner was delicious.

Our trip was not without difficulties, however. The group learned a bit more about self-regulation, governance and the balance of powers, as a consequence of “The Great Brownie Incident,” and the, “P.E. Fiasco.”

We were also fairly well cut off from the “cloud”: no internet, and you could only get cell reception if you were standing in the middle of the road in just the right spot in front of Cabin #3.

But more on these later. I have some sleep to catch up on.


View Coon Creek Immersion in a larger map

Life in Four Domains

The four domains of life, according to Boyer et al. (2010).

This wonderful, impressionistic image shows representatives of the three domains of life and large viruses, the proposed fourth.

This figure represents the living species in the four small pictures according to the current classification of organisms: eukaryotes (represented by yellow cell), bacteria (represented by green cell), Archaea (represented by blue cell) and viruses (represented by magenta colored Mimivirus).

— Boyer et al. (2010): Boyer M, Madoui M-A, Gimenez G, La Scola B, Raoult D (2010) Phylogenetic and Phyletic Studies of Informational Genes in Genomes Highlight Existence of a 4th Domain of Life Including Giant Viruses. PLoS ONE 5(12): e15530. doi:10.1371/journal.pone.0015530

Carl Zimmer has an excellent piece in Discover Magazine that summarizes the research, and sets out the new tree of life. Particularly important, is the fact that viruses can transfer genes with each other. The other domains tend to mix their genes during reproduction.

We are Stardust: Supernovas and the Heavy Elements

Expanding globe of debris from the explosion of Tycho's Star. Tycho Brahe observed the star as it went supernova about 540 years ago. The red is the debris, the stardust, created by the explosion. Image from NASA.

We could have been talking about the nuclear meltdowns in Japan, but I’m not sure. Our conversations tend to wander. I remember trying to explain where the carbon atoms, that are so essential for life, came from. It’s been a while since we saw this topic, so I figured it wouldn’t hurt to go it over again. And then I found this wonderful image of the Tycho supernova from the Chandra space telescope. Supernovas are where the heaviest atoms are formed.

In the beginning … the big bang created just the smallest elements, hydrogen and helium. But even these tiny things have gravity, so they pull each other together until there’s so much stuff that the pressure at the center of the clump is enough to fuse hydrogen atoms together.

Now fusion is easy to confuse with chemical bonding that occurs around us every day. After all, the hydrogen in the atmosphere is usually in the form of H2, which is two hydrogen atoms bonding together by shared electrons.

With fusion, on the other hand, the single protons that make up the nuclei of the hydrogen atoms are pushed together to create a bigger atom, helium. I say pushed together, because it takes a lot of pressure to fuse atomic nuclei. And it also releases a lot of energy. Notice all that heat and radiation that comes from the Sun? All that energy was created by the fusion of hydrogen atoms; the smallest element, hydrogen, fuels the stars.

Fusion of two hydrogen atoms to create helium, compared the chemical bonding of hydrogen atoms to produce hydrogen gas (H2). The nutrons are left out for clarity.

The huge amounts of energy released by fusion makes fusion power one of the holy grails of nuclear energy research. If we were able to create and control self-sustaining fusion reactions, just like what happens in the Sun, we would have a source of tremendous energy. There is a lot of research in this area. Some people have figured out how to build fusion reactors in their basements, but these use a lot more energy than they produce so they’re not very useful as a power plant (Barth, 2010). The ITER reactor, currently being built in France, aims to be the first to produce more electricity than it uses.

Now back to the stars. Hydrogen atoms fuse to form helium, but it takes a lot more pressure to create larger atoms: carbon has six protons, nitrogen seven, and oxygen eight. These elements are essential for life (as we know it). The only time stellar forces are great enough to produce these are when stars explode; an exploding star is said to have gone nova. Bigger atoms, like iron (26 protons), gold (79 protons), and uranium (92 protons) need even greater forces, forces that only occur when the largest stars go supernova.

DNA. (from Wikipedia)

So if these elements are only produced in novae and supernovae, how did they get to Earth? How did they get into your DNA?

Well when stars explode, a lot of these newly formed elements are blasted off into space. It’s a sort of cosmic dust. We could even call it stardust. It’s matter, just like the hydrogen and helium from the big bang, only bigger, which means they have more mass, which means they have more gravity.

Formation of the solar system (model).

The gravity pulls the stardust together with the hydrogen and helium sill floating around in space (there’s a lot of it), to form new stars, and, now that there are the larger elements to create them, rocks, asteroids, and planets.

So, if you think about it, some stars needed to have been formed, lived their lives (which consists of fusing hydrogen atoms until they run out), and exploded to create the matter that makes up the planets in our solar system and the calcium in our bones, the sodium in our blood, and the carbon in our DNA.

Notes:

1. Lots of information about Tycho’s Star on SolStation.com.

Trail of Tears State Park in Missouri

View over the Mississippi River from the scenic outlook in the Trail of Tears State Park. The outlook juts out over rocky bluffs, which allows you to see the flood plain across the river.

Driving through Missouri last week, I stopped at the Trail of Tears State Park, which may be an excellent place to study the post-colonial history of Native Americans (perhaps as part of our civil rights discussions), and observed the Mississippi River and its flood plain before it becomes engorged at its confluence with the Ohio River.

In 1830, President Andrew Jackson passed the Indian Removal Act, which called for the removal of American Indians living east of the Mississippi River to relocate west of the Mississippi River. …

While some of the Cherokees left on their own, more than 16,000 were forced out against their will. In winter 1838-39, an endless procession of wagons, horsemen and people on foot traveled 800 miles west to Indian Territory. Others traveled by boat along river routes. Most of the Cherokee detachments made their way through Cape Girardeau County, home of Trail of Tears State Park. While there, the Indians endured brutal conditions; they dealt with rain, snow, freezing cold, hunger and disease. Floating ice stopped the attempted Mississippi River crossing, so the detachments had to set up camps on both sides of the river. It is estimated that over 4,000 Cherokees lost their lives on the march, nearly a fifth of the population.

–Missouri Department of Natural Resources: Remembering an American Tragedy

The small museum at the main park building does a very good job of trying to dispassionately tell the tragic story.


View Trail of Tears State Park, MO in a larger map

Taking a break on the Nature Walk behind the park's museum.

There’s a short, 1 km nature walk behind the building that was nice on a beautiful, sunny day in early spring. Warm, with the trees just barely beginning to bud you can get a feel for the ridge-and-valley topography of the park, which is in stark contrast to the flat floodplain of the Mississippi on the other side of the river. The park’s roads weave up and down the ridges, and I wished I’d had my bike with me.

Barge going downstream on the Mississippi River, past the river-side campground.

This early in the year (mid-March) most of the campgrounds in the interior of the park seem to be closed, but there is one down on a beach of the Mississippi River that was empty but open. This one has electrical hookups which is not a bad thing if you have the place all to yourself.

The scenic outlook is a wooden platform that juts out through the trees so you can see across the Mississippi to the flat floodplain and farmland beyond. Sitting on a cliff of sedimentary rock (it looked like limestone from a distance), the outlook is high enough that you can just make out the shapes of old meander bends and ox-bow lakes.

It’s a small park, probably worth a visit for the museum, and the outlook is nice, but probably not somewhere you’ll want to spend the night unless some of the upland campgrounds are open.

The museum’s focus on the relocation of the Cherokee would be a nice followup to the pre-Columbian focus of the Chucalissa Museum in Memphis.

Cape Girardeau River Wall.

If you’re looking at river processes, you’ll probably also want to stop in Cape Giradeau, which boasts a fromidable wall to protect the downtown from the Mississippi River’s spring floods.