Drag the charges around.
The force field created by the interaction of two electric charges (one positive and one negative). The source is at http://soriki.com/fields/electric/.
Middle and High School … from a Montessori Point of View
Drag the charges around.
The force field created by the interaction of two electric charges (one positive and one negative). The source is at http://soriki.com/fields/electric/.
Using glowscript.org, we can now put vpython programs online. Here’s a first shot of the coil program:
http://www.glowscript.org/#/user/lurbano/folder/Private/program/magnet-coil.py
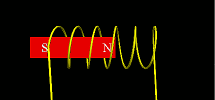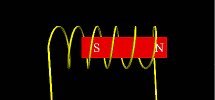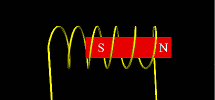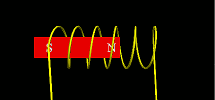
Some changes to the standard vpython language must be used and there are some limitations, but it seems to work.
Regardless, if learning is to be as efficient and deep as possible, it’s essential that it be done freely. That means giving children a voice in which activities to participate, for how long, and also the level of mastery they want to achieve. (“This is the biggest clash with traditional curriculum development,” Droujkova notes.)
— Vangelova (2014): 5-Year-Olds Can Learn Calculus
This article provides a lot of evidence to support the notion that the conceptual aspects of calculus and other “higher level” forms of math should be taught at all age levels, not just at the end of high school or in college.
The presentation below elaborates:
What happened:
Detailed article from Mashable: The poisoning of a city
A timeline from Michigan Radio: TIMELINE: Here’s how the Flint water crisis unfolded
An excellent, detailed program from Reveal: Do not drink: The water crisis in Flint, Michigan. The second part in particular is a good summary of the science issues.
A NPR summary from September 29th, 2015: High Lead Levels In Michigan Kids After City Switches Water Source
How to create ultra-cold temperatures (and what it tells us about the universe).
And this article (Below Absolute Zero: Negative Temperatures Explained) tells how to get below absolute zero.
Studying voltage and current in circuits can start with two laws of conservation.
Note: Some of the links are dead, but this MIT Opencourse pdf has a detailed explanation. And Kahn Academy has some videos on the current laws as well.
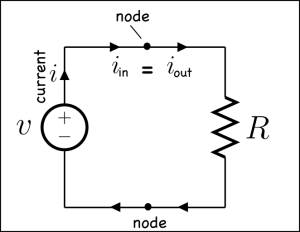
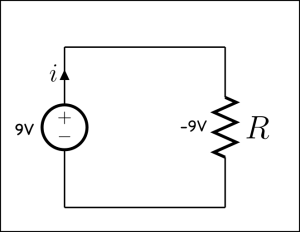
Things get more interesting when we get away from simple circuits.

Note that the convention for drawing diagrams is that the current move from positive (+) to negative (-) terminals in a battery. This is opposite the actual flow of electrons in a typical wired circuit because the current is a measure of the movement of negatively charged electrons, but is used for historical reasons.
Based on the MIT OpenCourseWare Introduction to Electrical Engineering and Computer Science I Circuits 6.01SC Introduction to Electrical Engineering and Computer Science Spring 2011.
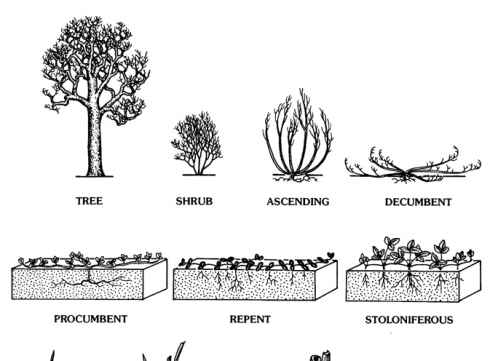
The vPlants Project. vPlants: A Virtual Herbarium of the Chicago Region. http://www.vplants.org is a wonderfully comprehesive collection of pictures with plant descriptions: plant form; leaf shapes; stem and leaf patterns; flower shapes; and more.
The Siege of Miami: A detailed report that looks at the increasing frequency of flooding in Miami, because of sea-level-rise. The reporter interviews a number of scientists and engineers who are not terribly optimistic about the long-term (50+ years) future of many Floridian cities because of the melting ice-caps in Greenland and Antarctica.
