OpenSCAD bills itself as “The Programmers Solid 3D CAD Modeller”. It does this job pretty well, which is probably why I like it so much. Like POV-RAY, which I’ve used before, you create primitive objects–spheres, boxes, cylinders, etc.–and add or subtract them from one another to create the three-dimensional shapes you want.
Unlike the more graphical 3d modeling programs, like SketchUp (which I’ve played with in the past), in OpenSCAD you have to specify in the script the exact dimensions of your primitives, and how to rotate them and translate them to get them where you want them to be in space. This makes it a great language to use in geometry class, or anywhere else you want students to learn about co-ordinate systems.
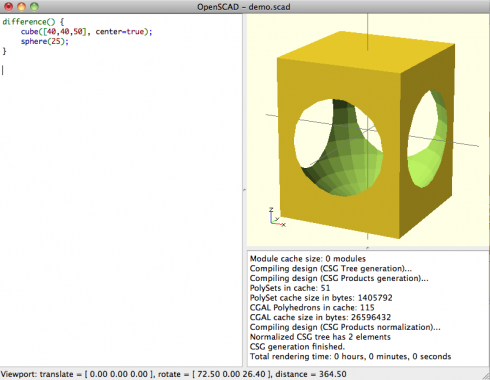
The script to create the box with a circle cut out of it (see figure above) is:
difference() {
cube([40,40,50], center=true);
sphere(25);
}
Vpython requires students of make similar geometric movements of their objects and renders them nicely in 3d, but given the incentive that they can print up a tangible result of their work, I’d be willing to bet that students, especially younger ones, would be quite motivated to work with OpenSCAD. Vpython does retain the advantage that it is able to do animations, while you can only print static objects. In addition, OpenSCAD is more of a scripting language than a programming language like Python (see some of my Vpython programs here).

The OpenSCAD documentation is quite good. I also found it easy to find instructions on how to create a 3d object from a black and white image, simply by extruding it in the third dimension (by iamwil on the Cubehero Blog and by I Heart Robotics).
One note: I’m using OSX 10.6.8 at the moment, and the current version of OpenSCAD does not work on it. Since I’m loathe to upgrade, I had to use the prior release of OpenSCAD-2013.06.dmg.