Projectile Motion

Abstract

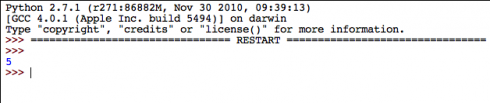
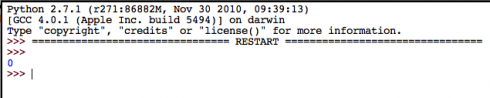
A series of still photographs of a projectile (soccer ball) in motion were used to determine the equation for the height of the ball (h(t) = 4.9 t² + 14.2 t + 1.25), the initial velocity of the ball (14.2 m), the maximum height of the ball (11.6 m), and the time between each photograph (0.41 s). The problem was solved numerically using MS Excel’s Solver function. There are much easier ways of doing this, which we did not do.

Introduction

projectile-diagram — Figure 1. Calculated elevation of the soccer ball after launch.

projectile-3832c2-800 — Figure 2. Animation of the soccer ball projectile.

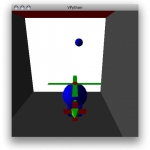
One of physics lab assignments I gave my students was to see if students could use a camera to capture a sequence of images of a projectile, plot the elevation of the projectile from the photographs, determine the constants in the parabolic equation for the height of the projectile, and, in so doing, determine the velocity at which the projectile was launched.

I offered my old, digital Pentax SLR that can take up to seven pictures in quick sequence and be set to fully manual. A digital video camera with a detailed timestamp would have been ideal, but we did not have one available at the time.

Now the easy way of getting the velocity data would be to estimate the heights (h) of the ball from the image using some sort of known reference (in this case the whiteboard), and determine the time between each photograph (Δt) by photographing a stopwatch using the same shutterspeed settings. After all, the average velocity of the ball between two images would be:

$! \bar{v} = \frac{\Delta h}{\Delta t}$

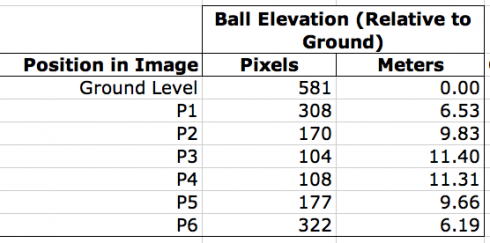
The reference whiteboard is four feet tall (1.22 m) in real life, but 51 pixels tall in the image. Using this ratio (i.e. 1.22 m = 51 px) we can convert the heights of the ball from pixels to meters:

elevations — Table 1. Table showing the conversion of the height of the ball in pixels to elevation (in meters).

Unfortunately, I think my students forgot to do the pictures of the stopwatch to get Δt, the time between each photograph. Since the lab reports are due on Monday, and it’s the weekend now I’m curious to see what they come up with.

However, I was wondering if they could use just the elevation data to back out the Δt. So I gave it a try myself. Even the easiest way of solving this problem is not trivial, in fact, I ended up resorting to Excel’s iterative solver to find the answers. While this procedure probably goes a little beyond what I expect from the typical high school physics student, more advanced students who are taking calculus might benefit.

Procedure

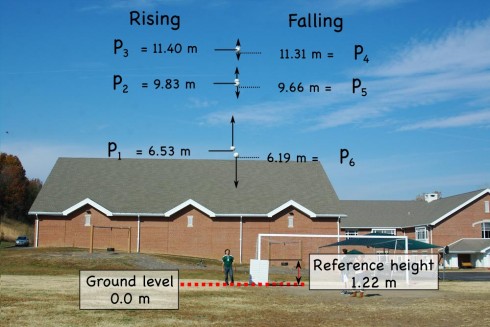
We took the reference whiteboard (1.21 m tall), a soccer ball, and the camera outside. The whiteboard was leant vertically against the post of the soccer goal. The ball was thrown vertically by a student standing next to the whiteboard (see Figure 1) while pictures were taken. The camera’s shutterspeed was 1/250th of a second. The distance from the camera to the person throwing the ball (and to the whiteboard) were not measured.

The procedure was repeated several times, but only one trail was used in this analysis.

The images were loaded onto a computer, and the program GIMP was used to determine the distance, in pixels, from the ground to the projectile. The size of the reference whiteboard, in pixels, was used to calculate the height of the soccer ball in meters.

The elevations measured off the photographs were then used to calculate the release velocity, time between snapshots, and maximum height of the ball.

The Equation for Elevation

I started with the fact that once the ball is released, the only force acting on it is the force of gravity. Since the mass of the ball does not change we only have to consider the acceleration due to gravity (-9.8 m/s²). I also neglect air resistance to make things easier.

Finding the Velocity Equation

Start with the fact that, acceleration is the rate of change of velocity with time. You can write it in the differential form:

$! a = \frac{dv}{dt} = -9.8$

so we integrate with respect to time to get the equation for velocity as a function of time:

$! v(t) = \int -9.8 dt$

$! v(t) = -9.8 t + c$

where c is an unknown constant. What we do know though, is that at the beginning, when the ball is just launched, time is zero (t = 0) so c_v becomes the initial velocity (v₀) at which the ball is thrown:

at t = 0, v(0) = v₀:
$! v_0 = -9.8 (0) + c$

$! v_0 = c$

So our velocity equation becomes:

$! v(t) = -9.8 t + v_0$

Finding the height equation

Now since we know that velocity is the rate of change of distance (in this case height) with time:

$! v(t) = \frac{dh}{dt} = -9.8 t + v_0$

so we integrate again to find the height equation:

$! \frac{dh}{dt} = -9.8 t + v_0$
$! h(t) = \int (-9.8 t + v_0) dt$
$! h(t) = \frac{-9.8 t^2}{2} + v_0 t + c$

Similar to what we did with the velocity equation, to find the new constant c we consider what happens at the start time, when the ball is launched, and t = 0 and h(0) = h₀;

$! h_0 = \frac{-9.8 (0)^2}{2} + v_0 (0) + c$

so:
$! h_0 = c$

The constant is equal to the initial height of the ball — the height of the ball when it’s thrown. So we end up with the final equation:

$! h(t) = \frac{-9.8 t^2}{2} + v_0 t + h_0$

Results

Solving all the unknowns

At this point, although we have an equation for the height of the ball, we don’t know the initial velocity (v₀), nor do we know the initial height of the ball when it’s released (h₀). And we still don’t know the time when the ball is at each position.

With that many unknowns we’d need the same number of independent equations to be able to solve for them all. It may be possible, but instead of analytically solving the equations I opted to take a numerical approach, and use Excel’s Solver function.

I started by setting up the equations to calculate the height of the ball at six different times to correspond with our six height measurements. It was necessary therefore to create a set of variables:

Time when we started taking pictures (t₁): Since we don’t know how long after we threw the ball we started taking pictures, I made this a variable called t₁.
The time between each picture (dt): I made the assumption that the time between each picture would be constant. The shutter speed was constant (1/250th of a second) so there is no obvious reason why the time should be different.
Initial velocity (v₀): The initial upward speed at which the ball was thrown. Obviously, the faster the initial speed the higher the ball goes, so this is a fairly important parameter.
Initial height (h₀): We also don’t precisely know how high the ball was when it was released, so this also needs to be a variable.

By defining the time between each picture as dt, we can write the time that each picture was taken in terms of the time of the initial picture (t₁) and dt. After all the second picture would have been taken dt seconds after the first for a total time of:

$! t(P2) = t_0 + dt$

similarly for all the pictures:

photo-times — Table 2. Table of expressions giving the time when each of the six photos were taken.

Now I set up an Excel spreadsheet and gave all the unknown variable values and initial value of 1:

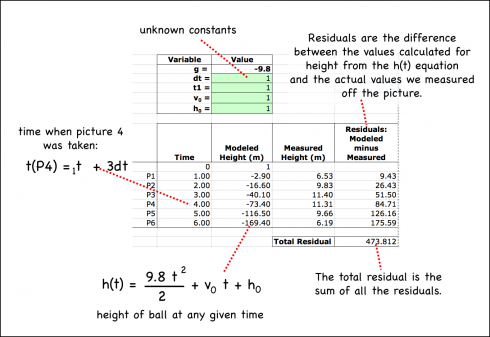
excel-solver — Table 3. Table in Excel for determining the height of a projectile. All of the unknown variables' values are highlighted in green and have been given an initial value of 1.

Now I just had to run Solver and tell it that I wanted the Total Residual, which gives the difference between the h(1) equation’s values for height and the actual, measured values, to be as close to zero as possible. A perfect fit of the equation to the data would have a total residual of one, but that’s not possible when you’re dealing with real data.

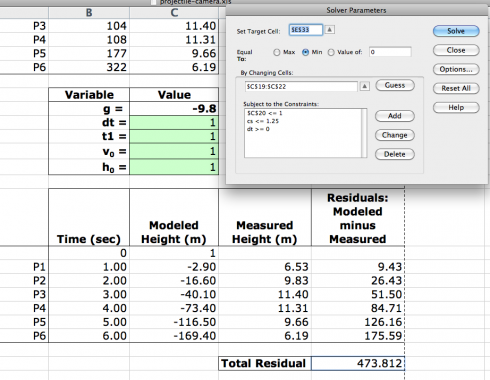
solving — Table 4. Parameters set in Solver to determine the values of the unknown constants.

Even so, I had to goose Solver a bit for it to produce reasonable numbers. I put in a few constraints:

dt >= 0: We could not have a negative time between pictures.
h₀ <= 1.25: 1.25 meters seemed reasonable for the height at which the ball was released.
t₁ <= 1: It also seemed reasonable that the time when the first picture was taken was less than one second after the ball was thrown.

I ran the Solver a few times, and had to reset dt to 0.5 at one point when it had become zero, but the final result looked remarkably good: the total difference between the modeled line and the actual data was only 0.113 meters.

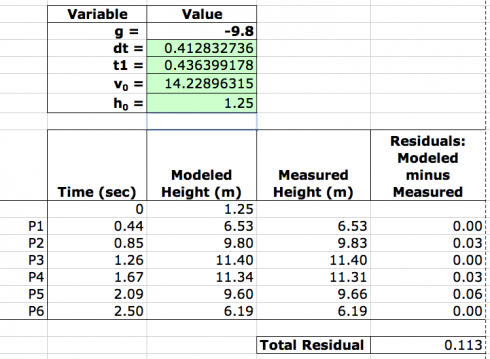
solver-after — Table 5. Solver's solution for the unknown constants in the height equation.

So we found that:

Initial velocity: v₀ = 14.2 m/s
Height at release: h₀ = 1.25 m
Time between pictures: dt = 0.41 s
Time when the first picture was taken: t₁ = 0.44 s

Which makes the height equation:

$! h(t) = \frac{-9.8 t^2}{2} + 14.2 t + 1.25$

Using these constants in the height equation, we could see how good fit the height equation was to the data:

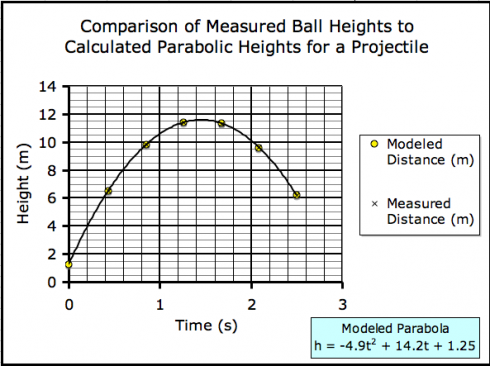
projectile-graph — Figure 3. Graph comparing the modeled heights (from the h(t) equation) to the actual data.

Maximum Height of the Ball

Finally, the maximum height of the ball can be read off the graph, but it can also be determined using the equation for the height of the ball:

$! h(t) = \frac{-9.8 t^2}{2} + v_0 t + h_0$

We know that the maximum height is reached when the ball stops moving upward and starts to descend. At that point, the vertical velocity of the ball is zero. Since the velocity of the ball is the rate of change of height ( $v = \frac{dh}{dt}$ ) we can differentiate the height equation to get an equation for velocity.

$! h(t) = \frac{-9.8 t^2}{2} + v_0 t + h_0$

$! v = \frac{dh}{dt} = -9.8 t + v_0$

since we’ve determined that the initial velocity of the ball is 14.2 m/s we get:

$! v = -9.8 t + 14.2$

when the velocity is zero (v = 0):

$! 0 = -9.8 t + 14.2$

which can be solved for t to find that the time the ball reaches it’s maximum height is:

$! t = 1.45 seconds$

Putting this into the height equation:

$! h(1.45) = \frac{-9.8 (1.45)^2}{2} + 14.2 (1.45) + 1.25$

gives:

$! h_{max} = 11.58 meters$

Discussion

I’m quite happy with the way this project turned out. The fit between the modeled heights (h(t)) and the actual heights was very good.

My primary concern going into the project was that the distortion from the camera lens would make this technique impossible, but that appears not to be a significant problem.

Most of this calculation, including the somewhat tricky numerical solution using Solver could have been avoided if I’d calibrated the camera, simply by pointing it at a stopwatch (using the same shutterspeed as in the experiment) and measuring the time between snapshots. It will therefore be interesting to see if the actual time between shots (dt) is close to the dt of 0.41 seconds calculated by the model.

Finally, as noted above, a video camera with a timestamp would possibly be a more useful technology for this experiment.

Conclusion

It is possible to analyze the projectile path of an object using a series of snapshots, to determine the initial velocity of the projectile, its release height, and the time between snapshots, if you can assume that the time between snapshots is identical. There are, however, much easier methods of solving this problem.

References

None, but this is where they’d be if I had any.

Appendix

The Excel spreadsheet where all the calculations were done is here.

Bird Poop: Force at Impact

In response to a question asked on the Car Talk radio program, Rhett Allain does the math to find out if falling bird poop can crack a windshield.

The answer: maybe. There are just a lot of assumptions that have to be made. Is falling bird poop spherical? What’s its density? How does the bird poop deform on impact? What is the compressive strength of automobile glass?

This is however an excellent real-life application of back-of-the-envelope physics and algebra. It required calculating:

the volume of the poop – extrapolated from the diameter of the residue on the windshield;
the terminal velocity of the poop – the velocity where gravity’s force is exactly counterbalanced by wind resistance so the poop is at its maximum speed;
the force of impact – calculated using the work done as the poop splatters;
and the pressure imparted by that force.

bird-poop — Brace for impact. Image by Marjie Kennedy.

Algebra in Programming, and a First Box

One of the first things you learn in algebra is to use variables to represent numbers. Variables are at the heart of computer programming, and in Python you can use them for more than just numbers. So open the IDLE text editor and get to work.

But first we’ll start with numbers. To assign a number to a variable you just write an equation. Here are a couple (you can copy and paste the code into the IDLE window, but usually typing it in yourself tends to be more meaningful and help you remember):

a = 2
b = 3

Now we can add these two variables together and create a new variable c.

a = 2
b = 3
c = a + b

Which is all very nice, but now we want our program to actually tell us what the result is so we print it to the screen.

a = 2
b = 3
c = a + b
print c

Run this program (F5 or select “Run Module” in the “Run” menu) to get:

first-prog-output — Output from the first program: 2+3=5.

Basic Operations and Types of Numbers

Now try some other basic operations:

+ and – are easy as you’ve seen above.

× : for multiplication use *, as in:

a = 2
b = 3
c = a * b
print c

÷ : to divide use a /, as in:

a = 2
b = 3
c = a / b
print c

Now as you know, 2 divided by 3 should give you two thirds, but the running this program outputs 0:

division-prog — 2 divided by 3 to gives 0 because Python thinks we're working with integers.

This is because the Python thinks you’re using integers (a whole number), so it gives you an integer result. If you want a fraction in your result, you need to indicate that you’re using real numbers, or more specifically, rational numbers, which can be integers or fractions, but usually show up as a decimal (these are usually referred to as floating point numbers in programming).

The easiest way to indicate that you don’t just want integers is to make one of your original numbers a decimal:

a = 2.0
b = 3
c = a / b
print c

which produces:

prog-decimal — Use a = 2.0 to indicate that we're using rational numbers.

Other Things Can Be Variables

In object oriented programming languages like Python you can assign all sorts of things to variables, not just numbers.

To create a box and give it a variable name you can use the program:

from visual import *
c = box()

which produces:

A box created with VPython. It looks much more interesting if you rotate it to see it in perspective.

box2 — A rotated, zoomed-out view of a box.

To rotate the view, hold down and drag the right mouse button. To zoom in or out, hold down the right and left buttons together and drag in and out. Mac users will probably have to use the “option” button to zoom, and the “command” button to rotate.

The line from visual import * tells the computer that it needs to use all the stuff in the module called “visual”, which has all the commands to make 3d objects (the “*” indicates all).

The c = box() line creates the box and assigns it a variable name of c. You don’t just have to use letters as variable names. In programming you want to use variable names that will remind you of what it’s supposed to represent. So you could just as well have named your variable “mybox” and gotten the same result:

from visual import *
mybox = box()

Now objects like this box have properties, like color. To make the box red you set the color property in one of two ways. The first method is to set the color as you create the object:

from visual import *
mybox = box(color = color.red)

The second is to set the property using the variable you’ve created and “dot” (.) notation.

from visual import *
mybox = box()
mybox.color = color.red

In both of these color.red is a variable name that the computer already knows because it was imported when you imported the “visual” module. There are a few other named colors like color.green and color.blue that you can find out more about in the VPython documentation (specifically here).

You can also find out about the other properties boxes have, like length, width and position (pos), as well as all the other objects you can create, such as springs, arrows and spheres.

At this point, its probably worth spending a little time creating new objects, and varying their properties.

Overview

We’ve just covered:

Assigning values to variables
Basic operations (+,-,×, and ÷)
Types of Numbers: Integers versus floating point
Assigning 3d objects to variables
Setting properties of 3d objects

Next we’ll try to make things move.

References

For how to install and run VPython, check here.

Algebra and Programming with VPython

Computer programming is the place where algebra comes to life. Students seem to get really excited when they write even the simplest instructions and see the output on the screen. I’m not sure exactly why this is the case, but I suspect it has something to do with being able to see the transition from abstract programming instructions to “concrete” results.

So I’ve decided to supplement my Algebra classes with an introduction to programming. I’m using the Python programming language, or, more specifically, the VPython variant of the language.

Why VPython? Because it’s free, it’s an easy-to-use high-level language, and it’s designed for 3d output, which seems to be somewhat popular these days. The oohs and aahs of seeing the computer print the result of a+b turn into wows when they create their first box. I’ve used the language quite a bit myself, and there are a lot of other interesting applications available if you search the web.

VPython was created to help with undergraduate physics classes, but since it was made to be usable by non-science majors, it’s really easy for middle and high school students to pick up. In fact, NCSU also has a distance education course for high school physics teachers. They also have some instructional videos available on YouTube that provide a basic introduction.

Helicopter_3rd_person — Image from a game created by middle school student Ryan W.

I use VPython models for demonstrations in my science classes, I’ve had middle school students use it for science projects, and I’ve just started my middle school algebra/pre-algebra students learning it as a programming language and they’re doing very well so far.

What I hope to document here is the series of lessons I’m putting together to tie, primarily, into my middle school algebra class, but should be useful as a general introduction to programming using VPython.

Getting VPython

You’ll need to install Python and VPython on your system. They can be directly downloaded from the VPython website’s download page for Windows, Macintosh or LINUX.

Once they’re installed, you’ll have the IDLE (or VIDLE) program somewhere on your system; a short-cut is usually put on the desktop of your Windows system. Run (double-click) this program and the VPython programming editor will pop up any you’re ready to go. You can test it by typing in something simple like:

a = 1
b = 2
c = a + b
print c

Then you run the program by going through the Run–>Run Module in the menu bar.

Which should cause a new window to pop up with:

Python 2.7.1 (r271:86882M, Nov 30 2010, 09:39:13) 
[GCC 4.0.1 (Apple Inc. build 5494)] on darwin
Type "copyright", "credits" or "license()" for more information.
>>> ================================ RESTART ================================
>>> 
3
>>>

Even better might be to test the 3d rendering, which you can do with the following program:

from visual import *

box()

which creates the following exciting image:

A box created with VPython. It looks much more interesting if you rotate it to see it in perspective.

To rotate the view, hold down and drag the right mouse button. To zoom in or out, hold down the right and left buttons together and drag in and out.

Lessons

Lesson 1: Variables, Basic Operations, Real and Integer Numbers and the First Box.

Lesson 2: Creating a graphical calculator: Coordinates, lists, loops and arrays: A Study in Linear Equations

The CoolMath Website

A colleague recommended the Cool Math website as something she uses as a supplement for her students. There are some games for the younger kids, and lessons in pre-algebra through algebra for secondary students. I’ve glanced through a few of the pre-algebra lessons, and like them. They’re short, fairly clearly written, and have good diagrams.

Algebra lessons at Coolmath.com

The site is also friendly to homeschoolers and their parents, with a decent teacher’s area that outlines the author’s perspective on teaching math.

Their Survivor Algebra is an interesting approach to encouraging peer teaching by breaking the class into “tribes” and giving bonus points on tests if all members of the tribe do well. I’m not sure I like the extrinsic motivation of the prizes and test score bonuses but I think there might be some good aspects of this type of classroom organization in very large classes.

It’s a very interesting site that’s worth investigating.

Concept Maps of Math

Algebra-PreAlgebra-Map-6-Ch01-1 — Introduction to algebra.

While it’s nice to have the math concepts arranged nicely based on their presentation in the textbook. Since my plan is to give just a few overview lessons and let students discover the details I’ll be presenting things a little differently based on my own conceptual organization. So I’ve created a second graphic map, which looks a bit disorganized, but gives links things by concept, at least in the way I see it.

Algebra-PreAlgebra-Map-6-copy — Concept map for an introduction to pre-Algebra based on the first chapter of the textbook, Pre-Algebra an Accelerated Course, by Dolciani et al., (1996).

This morning I presented just the first branch, about equations, expressions and variables. The general discussion covered enough to give the students a good overview of the introduction to Algebra. Tomorrow the pre-Algebra and Algebra topics will start to diverge, but I think today went pretty well.

We’ll see how it goes as we fill in the rest of the map.

Interactive Model showing the Kinetic Energy of a Gas

I really like this little video because it’s relatively dense with information but its visual cues complement each other quite nicely; the interactive model it comes from is great for demonstrations, but even better for inquiry-based learning. The model and video both show the motion of gas molecules in a confined box.

In the video, the gas starts off at a constant temperature. Temperature is a measure of how fast the particles are moving, but you can see the molecules bouncing around at different rates because the temperature depends on the average velocity (via Kinetic Energy), not the individual rates of motion. And if you look carefully, you notice the color of the particles depends on how fast they’re moving. A few seconds into the video, the gas begins to cool, and you can see the particles slow down and gradually the average color changes from blue (fast) to red and then some even fade out entirely.

In the interactive, VPython model I’ve put in a slider bar so you can control the temperature and observe the changes yourself. The model is nicely set up for introducing students to a few physics concepts and to the scientific method itself via inquiry-based learning: you can sit them down in front of the program, tell them it’s gas molecules in a box, have them observe carefully, record what they see, and then explain their observations. From there you can branch off into a lot of different places depending on the students’ interests.

Temperature (T) – a measure of the average kinetic energy (KE_average) of the substance. In fact, it’s proportional to the kinetic energy, giving a nice linear equation in case you want to tie it into algebra:
$! T = c {KE}_{average}$
where c is a constant.

Of course, you have to know what kinetic energy is to use this equation.
$! KE = \frac{1}{2} m v^2$
Which is a simple parabolic curve with m being the mass and v the velocity of the object.

The color changes in the model are a bit more metaphoric, but they come from Wein’s Displacement Law, which relates the temperature of an object, like a star, to the color of light it emits (different colors of light are just different wavelengths of light).

$! T = \frac{b}{l}$

where b is another constant and l is the wavelength of light. This is one of the ways astronomers can figure out the temperature of different types of stars.

Notes

The original VPython model, from Chabay and Sherwood’s (2002) physics text, Matter and Interactions, comes as a demo when you install their 3D modeling program VPython.

I’ve posted about this model before, but I though it was worth another try now that I have the video up on YouTube.

93 Ways to Prove Pythagoras’ Theorem

Pythagoras-2a-300 — Geometric proof of the Pythagorean Theorem by rearrangemention from Wikimedia Commons' user Joaquim Alves Gat. Animaspar.

Elegant in its simplicity but profound in its application, the Pythagorean Theorem is one of the fundamentals of geometry. Mathematician Alexander Bogomolny has dedicated a page to cataloging 93 ways of proving the theorem (he also has, on a separate page, six wrong proofs).

Some of the proofs are simple and elegant. Others are quite elaborate, but the page is a nice place to skim through, and Bogomolny has some neat, interactive applets for demonstrations. The Wikipedia article on the theorem also has some nice animated gifs that are worth a look.

Cut the Knot is also a great website to peruse. Bogomolny is quite distraught about the state of math education, and this is his attempt to do something about it. He lays this out in his manifesto. Included in this remarkable window into the mind of a mathematician are some wonderful anecdotes about free vs. pedantic thinking and a collection of quotes that address the question, “Is math beautiful?”

Mathematics, rightly viewed, possesses not only truth, but supreme beauty — a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show.

– Bertrand Russell (1872-1970), The Study of Mathematics via Cut the Knot.