Tag: genetics

I’m teaching a numerical methods class that’s partly an introduction to programming, and partly a survey of numerical solutions to different types of problems students might encounter in the wild. I thought I’d look into doing a session on genetic algorithms, which are an important precursor to things like networks that have been found to be useful in a wide variety of fields including image and character recognition, stock market prediction and medical diagnostics.

The ai-junkie, bare-essentials page on genetic algorithms seemed a reasonable place to start. The site is definitely readable and I was able to put together a code to try to solve its example problem: to figure out what series of four mathematical operations using only single digits (e.g. +5*3/2-7) would give target number (42 in this example).

The procedure is as follows:

• Initialize: Generate several random sets of four operations,
• Test for fitness: Check which ones come closest to the target number,
• Select: Select the two best options (which is not quite what the ai-junkie says to do, but it worked better for me),
• Mate: Combine the two best options semi-randomly (i.e. exchange some percentage of the operations) to produce a new set of operations
• Mutate: swap out some small percentage of the operations randomly,
• Repeat: Go back to the second step (and repeat until you hit the target).

And this is the code I came up with:

genetic_algorithm2.py

''' Write a program to combine the sequence of numbers 0123456789 and
    the operators */+- to get the target value (42 (as an integer))
'''

'''
Procedure:
    1. Randomly generate a few sequences (ns=10) where each sequence is 8
       charaters long (ng=8).
    2. Check how close the sequence's value is to the target value.
        The closer the sequence the higher the weight it will get so use:
            w = 1/(value - target)
    3. Chose two of the sequences in a way that gives preference to higher
       weights.
    4. Randomly combine the successful sequences to create new sequences (ns=10)
    5. Repeat until target is achieved.

'''
from visual import *
from visual.graph import *
from random import *
import operator

# MODEL PARAMETERS
ns = 100
target_val = 42 #the value the program is trying to achieve
sequence_length = 4  # the number of operators in the sequence
crossover_rate = 0.3
mutation_rate = 0.1
max_itterations = 400


class operation:
    def __init__(self, operator = None, number = None, nmin = 0, nmax = 9, type="int"):
        if operator == None:
            n = randrange(1,5)
            if n == 1:
                self.operator = "+"
            elif n == 2:
                self.operator = "-"
            elif n == 3:
                self.operator = "/"
            else:
                self.operator = "*"
        else:
            self.operator = operator
            
        if number == None:
            #generate random number from 0-9
            self.number = 0
            if self.operator == "/":
                while self.number == 0:
                    self.number = randrange(nmin, nmax)
            else:
                self.number = randrange(nmin, nmax)
        else:
            self.number = number
        self.number = float(self.number)

    def calc(self, val=0):
        # perform operation given the input value
        if self.operator == "+":
            val += self.number
        elif self.operator == "-":
            val -= self.number
        elif self.operator == "*":
            val *= self.number
        elif self.operator == "/":
            val /= self.number
        return val


class gene:

    def __init__(self, n_operations = 5, seq = None):
        #seq is a sequence of operations (see class above)
        #initalize
        self.n_operations = n_operations
        
        #generate sequence
        if seq == None:
            #print "Generating sequence"
            self.seq = []
            self.seq.append(operation(operator="+"))  # the default operation is + some number
            for i in range(n_operations-1):
                #generate random number
                self.seq.append(operation())

        else:
            self.seq = seq

        self.calc_seq()

        #print "Sequence: ", self.seq
    def stringify(self):
        seq = ""
        for i in self.seq:
            seq = seq + i.operator + str(i.number)
        return seq

    def calc_seq(self):
        self.val = 0
        for i in self.seq:
            #print i.calc(self.val)
            self.val = i.calc(self.val)
        return self.val

    def crossover(self, ingene, rate):
        # combine this gene with the ingene at the given rate (between 0 and 1)
        #  of mixing to create two new genes

        #print "In 1: ", self.stringify()
        #print "In 2: ", ingene.stringify()
        new_seq_a = []
        new_seq_b = []
        for i in range(len(self.seq)):
            if (random() < rate): # swap
                new_seq_a.append(ingene.seq[i])
                new_seq_b.append(self.seq[i])
            else:
                new_seq_b.append(ingene.seq[i])
                new_seq_a.append(self.seq[i])

        new_gene_a = gene(seq = new_seq_a)
        new_gene_b = gene(seq = new_seq_b)
                       
        #print "Out 1:", new_gene_a.stringify()
        #print "Out 2:", new_gene_b.stringify()

        return (new_gene_a, new_gene_b)

    def mutate(self, mutation_rate):
        for i in range(1, len(self.seq)):
            if random() < mutation_rate:
                self.seq[i] = operation()
                
            
            

def weight(target, val):
    if val <> None:
        #print abs(target - val)
        if abs(target - val) <> 0:
            w = (1. / abs(target - val))
        else:
            w = "Bingo"
            print "Bingo: target, val = ", target, val
    else:
        w = 0.
    return w

def pick_value(weights):
    #given a series of weights randomly pick one of the sequence accounting for
    # the values of the weights

    # sum all the weights (for normalization)
    total = 0
    for i in weights:
        total += i

    # make an array of the normalized cumulative totals of the weights.
    cum_wts = []
    ctot = 0.0
    cum_wts.append(ctot)
    for i in range(len(weights)):
        ctot += weights[i]/total
        cum_wts.append(ctot)
    #print cum_wts

    # get random number and find where it occurs in array
    n = random()
    index = randrange(0, len(weights)-1)
    for i in range(len(cum_wts)-1):
        #print i, cum_wts[i], n, cum_wts[i+1]
        if n >= cum_wts[i] and n < cum_wts[i+1]:
            
            index = i
            #print "Picked", i
            break
    return index

def pick_best(weights):
    # pick the top two values from the sequences
    i1 = -1
    i2 = -1
    max1 = 0.
    max2 = 0.
    for i in range(len(weights)):
        if weights[i] > max1:
            max2 = max1
            max1 = weights[i]
            i2 = i1
            i1 = i
        elif weights[i] > max2:
            max2 = weights[i]
            i2 = i

    return (i1, i2)
        
    
    
            


# Main loop
l_loop = True
loop_num = 0
best_gene = None

##test = gene()
##test.print_seq()
##print test.calc_seq()

# initialize
genes = []
for i in range(ns):
    genes.append(gene(n_operations=sequence_length))
    #print genes[-1].stringify(), genes[-1].val
    

f1 = gcurve(color=color.cyan)

while (l_loop and loop_num < max_itterations):
    loop_num += 1
    if (loop_num%10 == 0):
        print "Loop: ", loop_num

    # Calculate weights
    weights = []
    for i in range(ns):
        weights.append(weight(target_val, genes[i].val))
        # check for hit on target
        if weights[-1] == "Bingo":
            print "Bingo", genes[i].stringify(), genes[i].val
            l_loop = False
            best_gene = genes[i]
            break
    #print weights

    if l_loop:

        # indicate which was the best fit option (highest weight)
        max_w = 0.0
        max_i = -1
        for i in range(len(weights)):
            #print max_w, weights[i]
            if weights[i] > max_w:
                max_w = weights[i]
                max_i = i
        best_gene = genes[max_i]
##        print "Best operation:", max_i, genes[max_i].stringify(), \
##              genes[max_i].val, max_w
        f1.plot(pos=(loop_num, best_gene.val))


        # Pick parent gene sequences for next generation
        # pick first of the genes using weigths for preference    
##        index = pick_value(weights)
##        print "Picked operation:  ", index, genes[index].stringify(), \
##              genes[index].val, weights[index]
##
##        # pick second gene
##        index2 = index
##        while index2 == index:
##            index2 = pick_value(weights)
##        print "Picked operation 2:", index2, genes[index2].stringify(), \
##              genes[index2].val, weights[index2]
##

        (index, index2) = pick_best(weights)
        
        # Crossover: combine genes to get the new population
        new_genes = []
        for i in range(ns/2):
            (a,b) = genes[index].crossover(genes[index2], crossover_rate)
            new_genes.append(a)
            new_genes.append(b)

        # Mutate
        for i in new_genes:
            i.mutate(mutation_rate)
                

        # update genes array
        genes = []
        for i in new_genes:
            genes.append(i)


print
print "Best Gene:", best_gene.stringify(), best_gene.val
print "Number of iterations:", loop_num
##

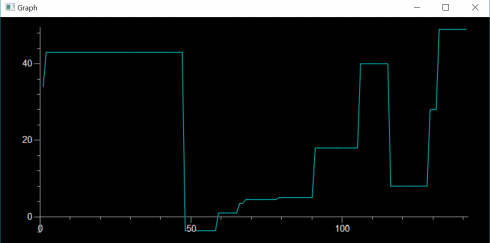
When run, the code usually gets a valid answer, but does not always converge: The figure at the top of this post shows it finding a solution after 142 iterations (the solution it found was: +8.0 +8.0 *3.0 -6.0). The code is rough, but is all I have time for at the moment. However, it should be a reasonable starting point if I should decide to discuss these in class.