A few of my students have been complaining that we don’t do enough different things from week to week for them to write a different newsletter article every Friday. PE, after all, is still PE, especially if we’re playing the same game this week as we did during the last.
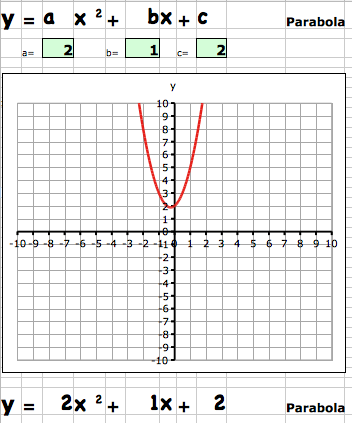
So I’ve been thinking of ways to disabuse them of the notion that anything can be boring or uninteresting in this wonderful, remarkable world. A world of fractal symmetry, where a variegated leaf, a deciduous tree and a continental river system all look the same from slightly different points of view. A counterintuitive world where the smallest change, a handshake at the end of a game, or a butterfly flapping its wings can fundamentally change the nature of the simplest and the most complex systems.
“Chaos is found in greatest abundance wherever order is being sought. It always defeats order, because it is better organized.”
— Terry Pratchett (Interesting Times)

There are two things I want to try, and I may do them in tandem. The first is to give special writing assignments where students have to describe a set of increasingly simple objects, with increasingly longer minimum word limits. I have not had to impose minimum word limits for writing assignments because peer sharing and peer review have established good standards on their own. Describing a tree, a coin, a 2×4, a racquetball in a few hundred words would be an exercise in observation and figurative language.
To do good writing and observation it often helps to have good mentor texts. We’re doing poetry this cycle and students are presenting their poems to the class during our morning community meetings. It had been my intention to make this an ongoing thing, so I think I’ll continue it, but for the next phase of presentations, have them chose descriptive poems like Wordsworth’s “Yew Trees“*.

The world is too interesting a place to let boredom get between you and it.