Middle and High School … from a Montessori Point of View
To avoid putting off work:
If children live with criticism, they learn to condemn.
If children live with hostility, they learn to fight.
If children live with fear, they learn to be apprehensive.
If children live with pity, they learn to feel sorry for themselves.
If children live with ridicule, they learn to feel shy.
…
If children live with encouragement, they learn confidence.
…
If children live with acceptance, they learn to love.
…
If children live with sharing, they learn generosity.
If children live with honesty, they learn truthfulness.
If children live with fairness, they learn justice.
If children live with kindness and consideration, they learn respect.
If children live with security, they learn to have faith in themselves and in those about them.–Nolte (1998): Children Learn What They Live via Children Learn What They Live: A Chronology of Different Versions.
I’ve always favored an apprenticeship (epistemological) model for teaching. Not so much learning facts, but learning how people with long experience in an area approach problems to be solved. So to have students do what scientists do (or historians for that matter), and to model how these experts think.
David Brook’s, The Social Animal, expresses this philosophy in a more narrative form:
Of course, Ms. Taylor wanted to impart knowledge, the sort of stuff that shows up on tests. But within weeks, students forget 90 percent of the knowledge they learn in class anyway. The only point of being a teacher is to do more than impart facts; it’s to shape the way students perceive the world, to help a student absorb the rules of a discipline. …
She didn’t so much teach them as apprentice them. Much unconscious learning is done through immitation. She exhibited ways of thinking through a problem and then hoped her students participated along with her.
She forced them to make mistakes. …
She tried to get students to interrogate their own unconscious opinions. …
She also forced them to work. …
— Brooks, D., 2012: The Social Animal.
New technology has a tendency to be used badly, but that does not mean it can’t be a powerful tool. Konstantin Kakaes argues that the increased use of technology is hurting science and math education.
A 2007 congressionally mandated study by the National Center for Educational Evaluation and Regional Assistance found that 16 of the best reading and mathematics learning software packages—selected by experts from 160 submissions—did not have a measurable effect on test scores.
— Kakaes (2012): Why Johnny Can’t Add Without a Calculator in Slate.
He makes some good points –a lot of technology is used employed simply because it’s “new technology” and not for what it can do– but I think he’s missing one fundamental aspect, probably because stuff is so new that we’re still figuring out how to use technology properly. The key missing aspect is that the increasing ubiquity of technology is changing who we are.
Technology is like an amplifier for our cognitive abilities –memorizing facts is less important because you can quickly look up the answers; how much time should you spend solving matricies if your can program your own matrix solver? –, and technology is becoming more closely integrated into who we are –we’re becoming inseparable from our smartphones (and it’s only a matter of time before they become implants).
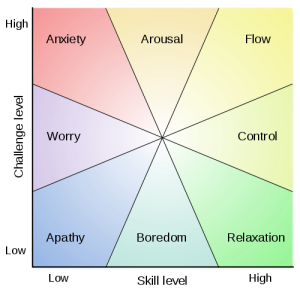
Three positives for every one negative is the minimum ratio required for people to flourish, according to the work of Marcial Losada (and others).
To flourish means to live within an optimal range of human functioning, one that connotes goodness, generativity, growth, and resilience.
— Fredrickson and Losada: Positive Affect and the Complex Dynamics of Human Flourishing (ᔥ PubMed), in American Psychologist (2005).
Why do we need more positives than negatives? Because we’re impacted more by negatives than positives, so we need more positives to offset. Note that people tend toward happiness on average.
Why are positive feelings good? Positivity increases:
In terms of education:
… initially positive attitudes—like interest and curiosity—produce more accurate subsequent knowledge than do initially negative attitudes—like boredom and cynicism. Positivity, by prompting approach and exploration, creates experiential learning opportunities that confirm or correct initial expectations. By contrast, because negativity promotes avoidance, opportunities to correct false impressions are passed by …. positive affect—by broadening exploratory behavior in the moment—over time builds more accurate cognitive maps of what is good and bad in the environment. This greater knowledge becomes a lasting personal resource.
— — Fredrickson and Losada: Positive Affect and the Complex Dynamics of Human Flourishing (ᔥ PubMed), in American Psychologist (2005).
So, once again, research shows how important it is to have a positive (happy) learning environment, and to be able to “spark the imagination” at the beginning of a lesson.
Cumulatively, there is the Losada Zone, a range from 3:1 to 11:1 of positive to negative feelings that are indicative of complex (good) interaction in groups, which separates people who flourish from those who languish.
Motivation is key to learning. Amabile and Kramer (2011) explain that strong motivation has been an essential driver in scientific discovery and the business world as well. They assert that:
Of all the things that can boost emotions, motivation, and perceptions during a workday, the single most important is making progress in meaningful work . And the more frequently people experience that sense of progress, the more likely they are to be creatively productive in the long run [my italics].— Amabile and Kramer, 2011: The Power of Small Wins in Harvard Business Review.
So for education, we need to design work so that students can be challenged (which makes it meaningful), yet be able to make good progress. It’s a delicate balance to get each student into their “flow zone“, where the work is neither too hard, nor too easy.
There’s been a push for students to take algebra earlier and earlier, yet there are some serious pedagogic arguments that early algebra might not be a great idea for many, if not most, students. A fascinating paper by Clotfelter et al., (2012) (pdf) showed pretty clearly that for a large number of students, taking algebra earlier actually resulted in worse performance in not just algebra, but the follow-up classes as well (geometry and pre-calculus for example), compared to students who waited to take the subject. Indeed the Charlotte-Mecklenburg School District (the district studied in the article) actually reversed their policy of having students take algebra in 8th grade.
Students affected by the acceleration initiative scored significantly lower on end-of-course tests in Algebra I, and were either no more likely or significantly less likely to pass standard follow-up courses, Geometry and Algebra II
— Clotfelter et al., (2012): The Aftermath of Accelerating Algebra: Evidence from a District Policy Initiative (pdf) via NY Fed.
The argument for early algebra comes from the correlation between early algebra and better performance on standardized tests, and more advanced math classes in high school. But the authors here indicate that forcing students to take algebra early does not result in the same outcomes.
The argument against early algebra is based on the research that shows formal thinking develops during adolescence, and the belief that to do well in algebra requires the abstract thinking skills that are seated in the maturing prefrontal cortex. Until students are ready for the abstract thinking required (which happens at different times for each student), they will struggle with algebra.
Algebra provides an essential foundation for further mathematics, which is why it is my strong preference that students progress by demonstrating mastery of the topics at their own pace rather than struggling through the class.
Having just had the chance to teach the entire upper (secondary) school math curriculum, I’ve been doing a little bit of necessary reflection on how to help students get interested. One of the key things we learned in the Montessori training was just how much more students learn when they’re self-motivated about a topic.
The common theme among all these classes was the use of the math to construct models to better understand the relationships between different things.
In Algebra I the focus is on linear models, like the one my middle schoolers drew from the results of their ice-melting experiment in science (see Figure 1). Another example (that I’ve not posted on yet) is calculating the density of liquids from a graph of volume and mass.
By the time they get to calculus they’re not just dealing with more complex functions, but they’re integrating and differentiating them to derive fundamental relationships.
Unfortunately, you usually end up with useful applications at the end of the book (or the chapter).
I wonder if it would not be more effective to put the examples in at the beginning. Not just in a little box for, “Why this is useful,” but start with the problem and then introduce the math need to solve it. A bit, perhaps, like Garfunkel and Mumford’s op-ed suggestion for more “real-life problems” in math education.