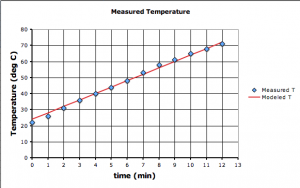
One of the first things that my pre-Calculus students need to learn is how to do a least squares regression to match any type of function to real datasets. So I’m teaching them the most general method possible using MS Excel’s iterative Solver, which is pretty easy to work with once you get the hang of it.
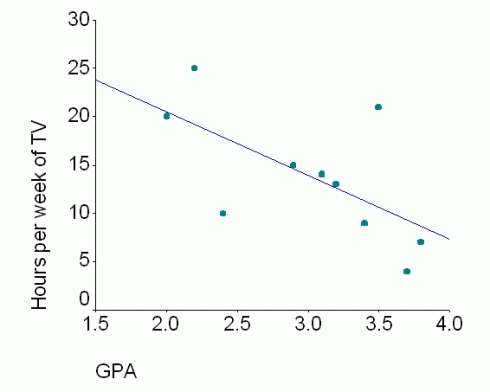
I’m teaching the pre-Calculus using a graphical approach, and I want to emphasize that the main reason we study the different classes of functions — straight lines, polynomials, exponential curves etc.— is because of how useful they are at modeling real data in all sorts of scientific and non-scientific applications.
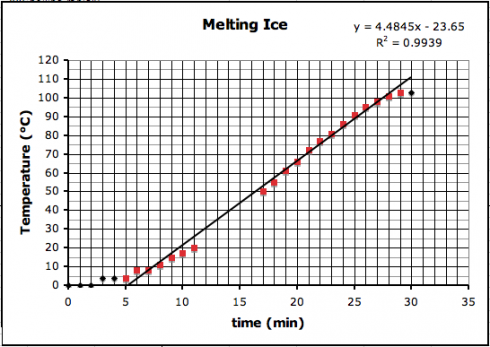
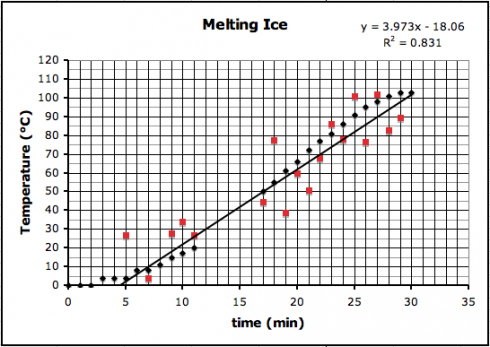
So I’m starting each topic with some real data: either data they collect (e.g. bring water to a boil) or data they can download (e.g. atmospheric CO2 from Mauna Loa). However, while it’s easy enough to pick two points, or draw a straight line by eye, and then determine its linear equation, it’s much trickier if not impossible when dealing with polynomials or transcendental functions like exponents or square-roots. They need a technique they can use to match any type of function, and least squares regression is the most commonly used method of doing this. While calculators and spreadsheet programs, like Excel, use least squares regression to draw trendlines on their graphs, they can’t do all the different types of functions we need to deal with.
The one issue that has come up is that not everyone has Excel and Solver. Neither OpenOffice nor Apple’s spreadsheet software (Numbers) has a good equivalent. However, if you have a good initial guess, based on a few datapoints, you can fit curves reasonably well by changing their coefficients in the spreadsheet by hand to minimize the error.
I’m working on a post on how to do the linear regression with Excel and Solver. It should be up shortly.
Notes
If Solver is not available in the Tools menu you may have to activate it because it’s an Add In. Wikihow explains activation.
Some versions of Excel for the Mac don’t have Solver built in, but you can download it from Frontline.