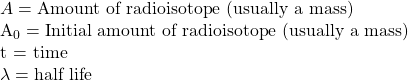Radioactive Half Lives

Since we most commonly talk about radioactive decay in terms of half lives, we can write the equation for the amount of a radioisotope (A) as a function of time (t) as:

  A = A_0 (\frac{1}{2})^\frac{t}{\lambda} 

where:
 A = \text{Amount of radioisotope (usually a mass)}  A_0 = \text{Initial amount of radioisotope (usually a mass)}   t = \text{time}  \lambda = \text{half life}

To reverse this equation, to find the age of a sample (time) we would have to solve for t:

Take the log of each side (use base 2 because of the half life):

  \log_2{(A)} = \log_2{  \left( A_0 (\frac{1}{2})^\frac{t}{\lambda} \right)} 

Use the rules of logarithms to simplify:

 \log_2{(A)} = \log_2{ ( A_0 )} + \log_2{  \left( (\frac{1}{2})^\frac{t}{\lambda} \right)}   

  \log_2{(A)} = \log_2{ ( A_0 )} +  \frac{t}{\lambda}  \log_2{   (\frac{1}{2}) }      

 \log_2{(A)} = \log_2{ ( A_0 )} +  \frac{t}{\lambda}  (-1)   

 \log_2{(A)} = \log_2{ ( A_0 )} -  \frac{t}{\lambda}      

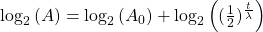
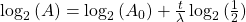
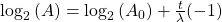
Now rearrange and solve for t:

 \log_2{(A)} - \log_2{ ( A_0 )} = -  \frac{t}{\lambda}      

 -\lambda \left( \log_2{(A)} - \log_2{ ( A_0 )} \right) = t      

  -\lambda \cdot \log_2{ \left( \frac{A}{A_0} \right)}  = t

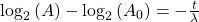
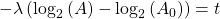
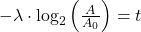
So we end up with the equation for time (t):

  t = -\lambda \cdot \log_2{ \left( \frac{A}{A_0} \right)}

Now, because this last equation is a linear equation, if we’re careful, we can use it to determine the half life of a radioisotope. As an assignment, find the half life for the decay of the radioisotope given below.

t (s)A (g)
0100
10056.65706876
20032.10023441
30018.18705188
40010.30425049
5005.838086287
6003.307688562

Leave a Reply