I hope you think that I am an acceptable writer, but when it comes to economics I speak English as a second language: I think in equations and diagrams, then translate.
I sometimes get the question: Why do I have to learn algebra? Followed by the statement: I’m never going to have to use it again. My response is that it’s a bit like learning to read; you can survive in society being illiterate, but it’s not easy. The same goes for algebra, but it’s a little more complex.
Paul Krugman argues for the importance of algebra for anyone thinking about economics, the economy, and what to do about it. Even at the basic level, economists think in mathematical equations and algebraic models, then they have to translate their thoughts into English to communicate them. People who are not familiar with algebra are at a distinct advantage.
There are important ideas … that can be expressed in plain English, and there are plenty of fools doing fancy mathematical models. But there are also important ideas that are crystal clear if you can stand algebra, and very difficult to grasp if you can’t. [my emphasis] International trade in particular happens to be a subject in which a page or two of algebra and diagrams is worth 10 volumes of mere words. That is why it is the particular subfield of economics in which the views of those who understand the subject and those who do not diverge most sharply.
P.S. In the article, he also points out the importance of algebra in the field of evolutionary biology.
Serious evolutionary theorists such as John Maynard Smith or William Hamilton, like serious economists, think largely in terms of mathematical models. Indeed, the introduction to Maynard Smith’s classic tract Evolutionary Genetics flatly declares, “If you can’t stand algebra, stay away from evolutionary biology.” There is a core set of crucial ideas in his subject that, because they involve the interaction of several different factors, can only be clearly understood by someone willing to sit still for a bit of math.
Having just had the chance to teach the entire upper (secondary) school math curriculum, I’ve been doing a little bit of necessary reflection on how to help students get interested. One of the key things we learned in the Montessori training was just how much more students learn when they’re self-motivated about a topic.
The common theme among all these classes was the use of the math to construct models to better understand the relationships between different things.
Figure 1. The rising temperatures in the middle of the graph can be modeled with a straight line. Graph by A.F.
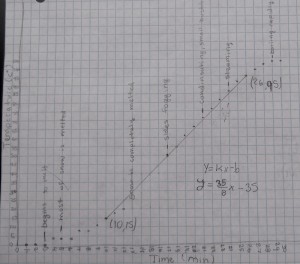
In Algebra I the focus is on linear models, like the one my middle schoolers drew from the results of their ice-melting experiment in science (see Figure 1). Another example (that I’ve not posted on yet) is calculating the density of liquids from a graph of volume and mass.
By the time they get to calculus they’re not just dealing with more complex functions, but they’re integrating and differentiating them to derive fundamental relationships.
Linearized graph of outflow rate versus the square root of time. From the draining water experiment.
Unfortunately, you usually end up with useful applications at the end of the book (or the chapter).
I wonder if it would not be more effective to put the examples in at the beginning. Not just in a little box for, “Why this is useful,” but start with the problem and then introduce the math need to solve it. A bit, perhaps, like Garfunkel and Mumford’s op-ed suggestion for more “real-life problems” in math education.
A ball rolling down a ramp hits a car which moves off uphill. Can you come up with an experiment to predict how far the car will move if the ball is released from any height? What if different masses of balls are used?
Students try to figure out the relationship between the ball's release height and how far the car moves.
For my middle school class, who’ve been dealing with linear relationships all year, they could do this easily if the distance the car moves is directly proportional to height from which the ball was released?
The question ultimately comes down to momentum, but I really didn’t know if the experiment would work out to be a nice linear relationship. If you do the math, you’ll find that release height and the maximum distance the car moves are directly proportional if the momentum transferred to the car by the ball is also directly proportional to the velocity at impact. Given that wooden ball and hard plastic car would probably have a very elastic collision I figured there would be a good chance that this would be the case and the experiment would work.
It worked did well enough. Not perfectly, but well enough.
Tool‘s Lateralus has the Fibonacci Sequence embedded into it. Ms. Wilson tells me that some of her Algebra II students were able to detect it out after listening to the song (a few times), but this video has the highlights where the sequence occurs.
One of my pre-Calculus students convinced me that the best way for him to learn how to work with matrices was for him to program a matrix solver. I helped him create a Gaussian Elimination solver in Python (which we’ve been using since last year).
Gaussian Elimination Matrix Solver by Alex Shine (comments by me).
from visual import *
'''The coefficient matrix (m) can be any sized square matrix
with an additional column for the solution'''
m = [ [1,-2,1,-4],[0,1,2,4],[2,3,-2,2]]
'''Convert the input matrix, m (which is a list) into an array'''
a = array(m,float)
print "Input matrix:"
print a
print
'''Get the shape of the matrix (number of rows and columns)'''
(r,c) = a.shape
rs = (1-r)
'''Solve'''
for j in range(r):
print "Column #:", j
for i in range(r):
if a[i,j] <> 0:
a[i,:] = a[i,:] / a[i,j]
print a
print
for i in range(rs+j,j):
if a[i,j] <> 0:
a[i,:] = a[j,:] - a[i,:]
print a
print
print "Solution"
for i in range (r):
a[i,:] = a[i,:] / a[i,i]
print "Variable", i, "=", a[i,-1]
print
print "Solution Matrix:"
print a
The code above solves the following system of equations:
x - 2y + z = -4
y + 2z = 4
2x + 3y - 2z = 2
Which can be written in matrix form as such:
You use the solver by taking the square matrix on the left hand side of the equation and combining it with the column on the hand side as an additional column:
This is entered into the program as the line:
m = [ [1,-2,1,-4],[0,1,2,4],[2,3,-2,2]]
When you run the above program you should get the results:
The matrix you put in can not have any zeros on its diagonal, so some manipulation is often necessary before you can use the code.
Other notes:
The negative zeros (-0) that show up especially in the solution matrix may not look pretty but do not affect the solution.
The code imports the vpython module in the first line but what it really needs is the numpy module, which vpython imports, for the arrays.
The next step is to turn this into a function or a class that can be used in other codes, but it’s already proved useful. My calculus students compared their solutions for the coefficients of a quadratic equation that they had to solve for their carpet friction experiment, which was great because their first answers were wrong.
A calculus student uses the matrix solver. Mr. Shine is now trying to convert the solver into an iPhone app.
Yesterday we used calculus to find the equation for the height of water in a large plastic water bottle as the water drained out of a small hole in the bottom.
Perhaps the most crucial point in the procedure was fitting a curve to the measured reduction of the water’s outflow rate over time. Yesterday, in our initial attempt, we used a straight line for the curve, which produced a very good fit.
Figure 1. The change in the outflow rate over time can be well approximated by a straight line.
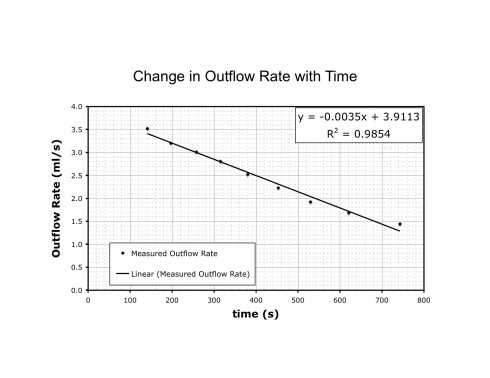
The R2 value is a measure of how good a fit the data is to the trendline. The straight line gives an R2 value of 0.9854, which is very close to a perfect fit of 1.0 (the lowest R2 can go is 0.0).
The resulting equation, written in terms of the outflow rate (dV/dt) and time (t), was:
However, if you look carefully at the graph in Figure 1, the last few data points suggest that the outflow does not just linearly decrease to zero, but approaches zero asymptotically. As a result, a different type of curve might be a better trendline.
Types of Equations
So my calculus students and I, with a little help from the pre-Calculus class, tried to figure out what types of curves might work. There are quite a few, but we settled for looking at three: a logarithmic function, a reciprocal function, and a square root function. These are shown in Figure 2.
Figure 2. Example curves that might better describe the relationship between outflow and time.
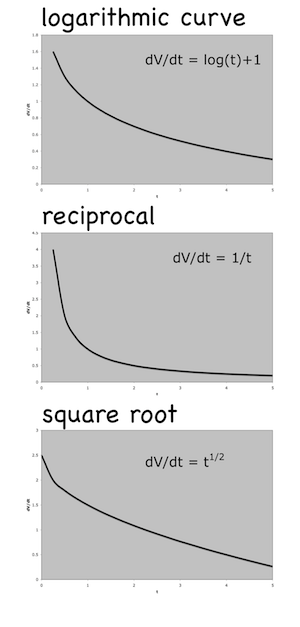
I steered them toward the square root function because then we’d end up with something akin to Torricelli’s Law (which can be derived from the physics). A basic square root function for outflow would look something like this:
the a coefficient stretches the equation out, while the b coefficient moves the curve up and down.
Fitting the Curve
Having decided on a square-root type function, the next problem was trying to find the actual equation. Previously, we used Excel to find the best fit straight line. However, while Excel can fit log, exponential and power curves, there’s no option for fitting a square-root function to a graph.
To get around this we linearized the square-root function. The equation, after all, looks a lot like the equation of a straight line already, the only difference is the square root of t, so let’s substitute in:
to get:
Now we can get Excel to fit a straight line to our data, but we have to plot the square-root of time versus temperature instead of the just time versus temperature. So we take the square root of all of our time measurements:
Time
Square root of time
Outflow rate
t (s)
t1/2 = x (s1/2)
dV/dt (ml/s)
0.0
0
3.91
45.5
6.75
3.52
97.8
9.89
2.94
140.9
11.87
3.52
197
14.04
3.21
257
16.05
3.01
315.1
17.75
2.81
380.1
19.50
2.53
452.9
21.28
2.23
529.6
23.01
1.92
620.7
24.91
1.69
742.7
27.25
1.45
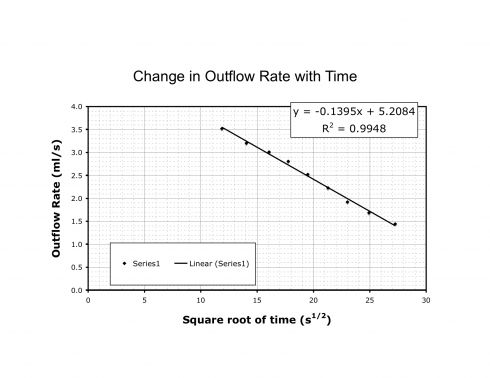
We can now plot the outflow rate versus the square root of time (Figure 3).
Figure 3. Linear trend relating the outflow rate to the square root of time. The regression coefficient (R2) of 0.9948 is better than the simply linear trend of outlfow rate versus time (which was 0.9854).
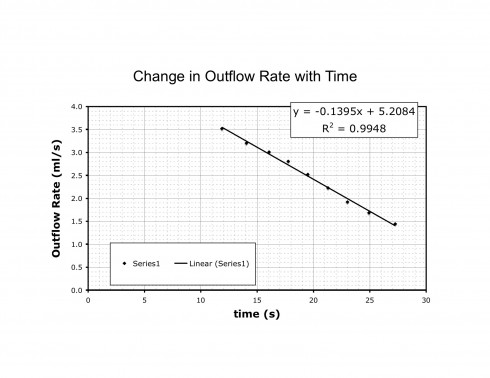
The equation Excel gives (Figure 3), is:
and we can substitute back in for x=t1/2 to get:
Getting back to the Equation for Height
Now we can do the same procedure we did before to find the equation for height.
First we substitute in V=πr2h:
Factor out the πr2 and move it to the other side of the equation to solve for the rate of change of height:
Then integrate to find h(t) (remember) :
gives:
which might look a bit ugly, but that’s only because I haven’t simplified the fractions. Since the radius (r) is 7.5 cm:
Finally we substitute in the initial value (t=0, h=11) to solve for the coefficient:
giving the equation:
Plotting the equations shows that it matches the measured data fairly well, although not quite as well as when we used the previous linear function for outflow.
Figure 4. Integrating a square root function for the outflow rate gives a modeled function for the changing height over time that slightly undermatches the measured heights.
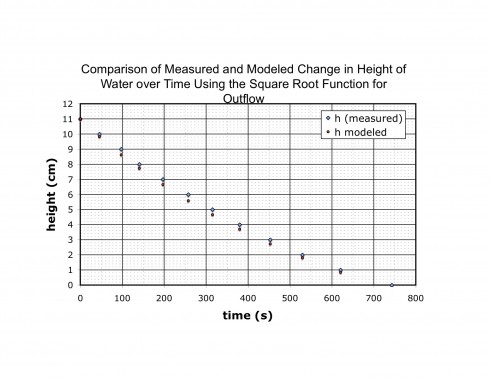
Discussion
I’m not sure why the square root function for outflow does not give as good a match of the measurements of height as does the linear function, especially since the former better matches the data (it has a better R2 value).
It could be because of the error in the measurements; the gradations on the water bottle were drawn by hand with a sharpie so the error in the height measurements there alone was probably on the order of 2-3 mm. The measurement of the outflow volume in the beaker was also probably off by about 5%.
I suspect, however, that the relatively short time for the experiment (about 15 minutes) may have a large role in determining which model fit better. If we’d run the experiment for longer, so students could measure the long tail as the water height in the bottle got close to the outlet level and the outflow rate really slowed down, then we’d have found a much better match using the square-root function. The linear match of the outflow data produces a quadratic equation when you integrate it. Quadratic equations will drop to a minimum and then rise again, unlike the square-root function which will just continue to sink.
Conclusions
The linearization of the square-root function worked very nicely. It was a great mathematical example even if it did not produce the better result, it was still close enough to be worth it.
I punched a small hole (about 1mm radius) in a one gallon plastic bottle and had my students measure the rate at which water drained. Even though the apparatus and measurement technique was fairly rough, we were able to, with a little calculus, determine the equation for the height of the water in the bottle as a function of time.
Figure 1. A student uses a stopwatch to measure the outflow rate of water from the plastic bottle.
Introduction
Questions about water draining from a tank are a pretty common in calculus textbooks, but there is a significant difference between seeing the problem written down, and having to figure it out from a physical example. The latter is much more challenging because it does not presuppose any relationships for the change in the height of water with time; students must determine the relationship from the data they collect.
The experimental approach mimics the challenges faced by scientists such as Henry Darcy who first determined the formulas for groundwater flow (Darcy, 1733) almost 300 years ago, not long after the development of modern calculus by Newton and Leibniz (O’Conner and Robertson, 1996).
Procedure
Figure 2. The apparatus.
I punched a small hole, about 1mm in radius, in the base of a plastic, one-gallon bottle. I chose this particular type of bottle because the bulk of it was cylindrical in shape.
Students were instructed to figure out how the rate at which water flowed out (outflow rate) changed with time, and how the height of the water (h) in the bottle changed with time. These relationships would allow me to predict the outflow rate at any time, as well as how much water was left in the container at any time.
Data collection:
To measure height versus time, we marked the side of the bottle (within the cylindrical region) in one centimeter increments and recorded the time it took for the water level to drop from one mark to the next. There were a total of 11 marks.
To measure the outflow rate, we intercepted the outflow using a 25 ml beaker (not shown in Figure 2), and measured the time it took to fill to the 25 ml mark.
Results
Time elapsed since last measurement
Height of water in container
Time to fill 25ml beaker
Δt (s)
h (cm)
tf (s)
0.0
11
6.4
45.5
10
7.1
52.3
9
8.5
43.1
8
7.1
56.1
7
7.8
60.6
6
8.3
57.6
5
8.9
65.0
4
9.9
72.8
3
11.2
76.7
2
13.0
91.1
1
14.8
122.0
0
17.3
Table 1: Outflow rate, water height change with time.
To analyze the data, we calculated the total time (the cumulative sum of the elapsed time since the previous measurement) and the outflow rate. The outflow rate is the change in volume with time:
So our data table becomes:
Time
Height of water in container
Outflow rate
t (s)
h (cm)
dV/dt (ml/s)
0.0
11
3.91
45.5
10
3.52
97.8
9
2.94
140.9
8
3.52
197
7
3.21
257
6
3.01
315.1
5
2.81
380.1
4
2.53
452.9
3
2.23
529.6
2
1.92
620.7
1
1.69
742.7
0
1.45
Table 2. Height of water and outflow rate of the bottle.
The graph of the height of the water with time shows a curve, although it is difficult to determine precisely what type of curve. My students started by trying to fit a quadratic equation to it, which should work as we’ll see in a minute.
Figure 3. The decrease in height with time is not a straight line (is non-linear).
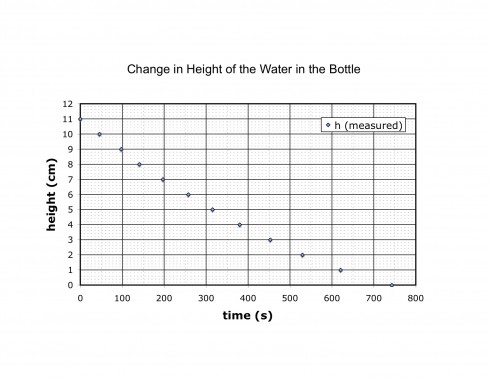
The plot of the outflow rate versus time, however, shows a pretty good linear trend. (Note that we do not use the first three datapoints (in Table 2), which we believe are erroneous because we were still sorting out the measuring method.)
Although I’ll note here that the data should ideally be modeled using a square root equation (Torricelli’s Law), that is beyond the present scope of the problem (we’ll try that tomorrow as a follow exercise).
Plotting the data in Excel we could add a linear trendline.
Figure 4. The outflow rate decreases linearly with time.
For the linear trendline, Excel gives the equation:
The y-axis is outflow rate (the change in volume with time), and the x axis is time (t), so the linear equation becomes:
Notice that this is a differential equation.
To determine the rate of at which the height of water in the container is changing, we need to recognize that the container is cylindrical in shape, and the volume (V) of a cylinder depends on its radius (r) and height (h):
which can be substituted into differential in the rate equation:
since π and the radius (r) are constants (since the jug’s shape is a cylinder), they can be pulled out of the differential:
Dividing through by πr2 solves for the rate of change of height:
Isolating the coefficients gives:
This equation should give the rate at which the height changes with time, however, if you look at it carefully you’ll realize that for the time range we’re using (less than 800 seconds) the value of dh/dt will always be positive. We correct this by recognizing that the outflow rate is a loss of water, so a positive outflow should result in a negative change in height, therefore we rewrite the equation as:
which gives:
Now comes the calculus
Now, we can use this rate equation to find the equation for height versus time by integrating with respect to time:
to get:
And all we have to do to the find the constant of integration is substitute in a known point, an initial value. As is often the case, the best point to use is the starting point where t=0 makes the rest of the calculations easier. In our case, when t=0, h=11:
so:
And our final equation becomes:
which is a quadratic equation as my students guessed before we did the calculus.
Does it work?
You will notice that in the math above, we never use the height data in determining equation for height versus time; all the calculations are based on the trendline for the outflow rate versus time.
As a result, we can compare the results of our equation to the actual measurements to see if our calculations are even close. Remarkably, they are.
Figure 5. The results from our equation (modeled) match the measured heights so well, the data points are difficult to distinguish on the graph.
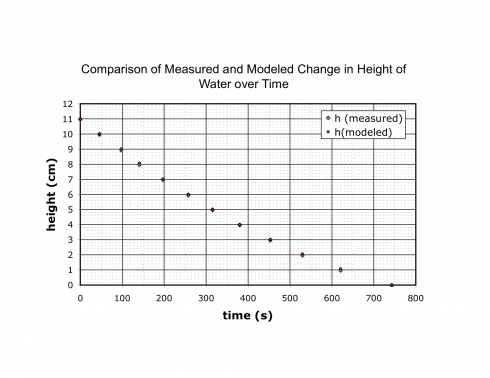
Discussion
Despite all the potential for error, particularly, our relatively crude measurement techniques, and the imperfect cylindrical shape of our plastic bottle, the experiment went remarkably well.
Students found it quite challenging, and required some assistance even though this is a problem they have seen before in their textbook.
The problems in the textbook use Torricelli’s Law, which should much better describe the draining of a tank than the linear equation we find for dV/dt.
Torricelli’s Law:
where a is the area of the outlet hole, and g is the acceleration due to gravity.
In our actual experiment it is difficult to tell that a square root function would work better. Excel does not have an option for matching a square root function, so the calculations would become more involved (although it could be set up using Excel’s iterative solver or Goal Seek function).
Conclusion
Our experiment to use calculus to determine the rate of change of the height of water in a leaking plastic water bottle was a successful exercise even though the roughness of the data collection did not permit identification of the square root law for leakage.
Walter Russell Mead (and his commenters) highlight two articles (here and here) on Virginia Tech’s excellent computer-based learning setup for their mathematics classes. Most of the work is done on the computer, either at home or in a shared Math Emporium where teachers are available to help when necessary; which, except for the computer work, is very much like how my class works. It seems close to the ideal way of using technology to allow flexibility in learning and assessment, and is in many ways similar to New York City’s School of One program.
VT’s approach requires some self-motivation on the part of the students — students are able to use the 24 hour a day Emporium at any time — but the model should fit be a good fit for Montessori middle and high-school students who have much independence in managing how they use their time during the day.
Their assessment method also nice as it allows students to pace themselves and take their tests when they’re ready. It is based on students proving that they’ve learned the material — how they learned it is not important, nor is how many practice tests they took before they get to the test.
Each course is broken up into a series of “modules,” available on Emporium computers or the Internet, that students are required to complete within a certain amount of time. Each module outlines a specific set of mathematic principles and concepts. These are translated into specific examples to review and problems to solve.
Once the module materials are completed, students can take randomly generated practice tests that draw on a central bank of thousands of potential questions. If they get questions wrong, the computer refers them back to the appropriate materials, and there’s no limit to the number of practice tests they can take. When they decide they’re ready, students come to the Emporium to take an official, proctored test that’s generated in exactly the same way as the practice quizzes. Then they move to the next module. Instead of marking progress by time—the number of hours spent in proximity to a lecturer—Emporium courses measure advancement by evidence of learning.
![\left[ \begin{array}{ccc} 1 & -2 & 1 \\ 0 & 1 & 2 \\ 2 & 3 & -2 \end{array} \right] \left[ \begin{array}{c} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{c} -4 \\ 4 \\ 2 \end{array} \right]](https://MontessoriMuddle.org/wp-content/ql-cache/quicklatex.com-d7c93a4faec058d3b5dda1831bdeaca7_l3.png "Rendered by QuickLaTeX.com")
![\left[ \begin{array}{cccc} 1 & -2 & 1 & -4 \\ 0 & 1 & 2 & 4\\ 2 & 3 & -2 & 2\end{array} \right]](https://MontessoriMuddle.org/wp-content/ql-cache/quicklatex.com-d2316bca341c565fbeab22075f4e2d73_l3.png "Rendered by QuickLaTeX.com")
) :
