Category: Mathematics

Polynomials: Revisiting pre-Kindergarten

Working with the thousand cube, hundred square, ten bar and unit cells in algebra.

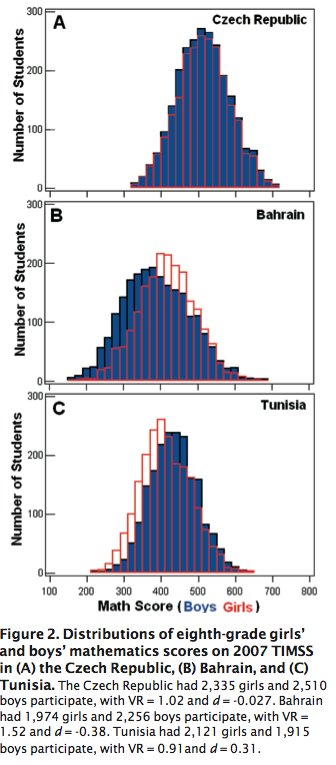
I sent a couple of my algebra students down to the pre-Kindergarten classroom to burrow one of their Montessori works. They were having a little trouble adding polynomials, and the use of manipulatives really helped.

The basic idea is that when you add something like:

n^2 + 2n + 3n^2 + 4n + 5 + 2n^3 + 4 + 3n^3

you can’t add a n3 term to a n2 or a n term. You only combine the terms with the same degree (and same variables). So the equation above becomes:

2n^3 + 3n^3 + n^2 + 3n^2 + 4n + 2n + 5 + 4

which simplifies to:

5n^3 + 4n^2 + 6n + 9

The kids actually enjoyed the chance to run downstairs to burrow the materials from their old pre-K teacher (and weren’t they quite good about returning the materials when they were done with them).

And it clarifies a lot of misconceptions when you can clearly see that that you just can’t add a thousand cube to a ten bar — it just doesn’t work.

Gravity, the Electromagnetic Forces, and the Inverse Square Law

Calculating the forces between two charged particles (electric force), two magnets (the magnetic force), and two masses (the gravitational force) require remarkably similar equations. But, while electricity and magnetism are directly related (that’s why it’s called electromagnetism), gravity is its own fundamental force. Yet they all depend (inversely) on the square of the distance between the two objects creating the force, so they’re all said to obey some form of the inverse square law.

Gravitational Force (Fg)

The force exerted by two masses on one another is:

F_g = G \frac{m_1 m_2}{d^2}

where:

  • G is the gravitational constant (6.67300 × 10-11 m3 kg-1 s-2
  • m1 and m2 are the masses of the two objects attracting one another.
  • d is the distance between the two objects.

Electrical Force (Fe)

The force exerted by two electrically charged objects on one another (like a proton and an electron), is:

F_e = K \frac{q_1 q_2}{d^2}

where:

  • K is the electrical constant, sometimes called Coulumn’s constant (8.9876 × 109 N m2 C-2
  • q1 and q2 are the sizes of the charges (in Coulumbs) of the two objects attracting one another.
  • d is the distance between the two objects.

Magnetic Force (Fm)

The force exerted by two magnets on one another, is:

F_m = \mu \frac{p_1 p_2}{d^2}

where:

  • μ is a constant, (a little simplified)
  • p1 and p2 are strengths of the magnetic poles of the two objects attracting one another.
  • d is the distance between the two objects.

The magnetic force is a little more difficult to give a single equation for, because you need to factor in the shape of the magnets.

Inverse Square Laws

In addition to gravity, electric, and magnetic forces, light (which is electromagnetic radiation) and sound also obey inverse square laws.

Boys vs. Girls in Math: The Difference is Only Cultural

Boys tend to be better at math. That’s been the stereotype, but a new study (Kane and Mertz, 2011) published in the Notices of the American Mathematical Society provides evidence that, at all levels, it’s only because society and culture tend to support, and advance the stereotype.

… we conclude that gender equity and other sociocultural factors, not national income, school type, or religion per se, are the primary determinants of mathematics performance at all levels for both boys and girls. … It is fully consistent with socioeconomic status of the home environment being a primary determinant for success of children in school.

— Kane and Mertz, 2011: Debunking Myths about Gender and Mathematics Performance in Notices of the American Mathematical Society.

Kane and Mertz compared math achievement in a number of countries. If there were some genetic reason for different math abilities then boys should be better than girls everywhere. This is not the case. In more wealthy countries where there is more equality between the genders, the mathematics performance gap disappears.

In poorer countries like Tunisia boys tend to do better at math, while in rich ones like Barhrain girls do better. However, in places with greater equity between the genders, like the Czeck Republic, boys and girls do equally well. Figure from Kane and Mertz (2011).

Math & Art Contest

The Missouri Council of Teachers of Mathematics (MoCTM) has a Math & Art Contest that focuses on Geometry. It has fairly simple expectations, and it’s aimed at Middle School students and lower. The tie between the math and the art does not require much depth, but that’s probably appropriate for students who are still developing abstract thinking.

A tessellation. Image via Wikipedia.

I’m usually a bit cautious about the utility of contests. Their primary benefit is in the work that they motivate, not the reward (or hope of a reward) at the end; although, students do need to learn to win or lose with equanimity.

Equations of a Parabola: Standard to Vertex Form and Back Again

Highlighting the Vertex Form of the equation for a parabola.

The equation for a parabola is usually written as:

Standard form:
! y = ax^2 + bx + c

where a, b and c are constants. This is the form displayed in both the VPython Parabola and Excel parabola programs. However, to make the movement of the curve easier, the VPython program also uses the vertex form of the equation internally:

Vertex Form:
! y = a(x-h)^2 + k

where the point (h, k) is the location of the vertex of the parabola. In the example above, h = 1 and k = 2.

To translate between the two forms of the equation, you have to rewrite them. Start by expanding the vertex form:

y = a(x – h)2 + k

becomes:

y = a(x – h)(x – h) + k

multiplied out to get:

y = a(x2 – 2hx + h2) + k

now distribute the a:

y = ax2 – 2ahx + ah2 + k

finally, group all the coefficients:

y = (a)x2 – (2ah)x + (ah2 + k)

This equation has the same form as y = ax2 + bx + c if:

Vertex to Standard Form:

a = a
b = -2ah
c = ah2+k

And we can rearrange these equations to go the other way, to find the vertex form from the standard form:

Standard to Vertex Form:

! a = a
! h = \frac{\displaystyle -b}{\displaystyle 2a}
! k = c - ah^2 = c - \frac{\displaystyle b^2}{\displaystyle 4a}

Summary

In sum, you can write the standard equation for a parabola as:

Standard form:

And you can write the equation for the same parabola in vertex form as:

Vertex form:

UPDATES

UPDATE 1: This app will automatically convert from standard to vertex form (or back again).

UPDATE 2: Automatically generate and embed graphs using this parabolic grapher app.

Parabola Program

Animation showing the widening and shrinking of the parabola.

So I put together this interactive parabola program using VPython (code here) for students encountering these curves in Algebra.

Simple Excel program to graph a parabola.

It’s a more interactive version of the Excel parabola program in that you can move the curve by dragging on some control points, rather than just having to enter the coefficients of the equation. The program is still in development, but it is at a useful stage right now, so I thought I’d make it available for anyone who wanted to try it.

The program is fairly straightforward to use. You can move the curve (translate it) up and down, and expand or tighten the area within the parabola.

The program also displays the equation of the curve in standard form:
! y = ax^2 + bx + c

.

What the buttons do.

Next Steps

I’m also working making the standard equation editable by clicking on it and typing, and am considering showing the x-axis intercepts, which will give algebra students a nice, visual way to of checking their factoring.

References

Coffman, J., 2011 (accessed). Translating Parabolas. http://www.jcoffman.com/Algebra2/ch5_3.htm

Math Warehouse, 2011 (accessed). Equation of a Parabola
Standard Form and Vertex Form Equations, http://www.mathwarehouse.com/geometry/parabola/standard-and-vertex-form.php#

WolframAlpha.com, 2011 (accessed). http://www.wolframalpha.com/input/?i=a^2+x^4%2Bx^2-r^2%3D0

Sub-atomic Physics: The Significance of 0.8%

When it comes to particle physics … [m]easuring something once is meaningless because of the high degree of uncertainty involved in such exotic, small systems. Scientists rely on taking measurements over and over again — enough times to dismiss the chance of a fluke.

— Moskowitz (2011): Is the New Physics Here? Atom Smashers Get an Antimatter Surprise in LiveScience

New research, out of the Large Haldron Collider in Switzerland, shows a 0.8% difference in the way matter and antimatter particles behave. This small difference could go a long way in explaining why the universe is made up mostly of matter today, even though in the beginning there were about equal amounts of matter and antimatter. It would mean that the current, best theory describing particle physics, the Standard Model, needs some significant tweaking.

The Standard Model of elementary particles. The LHC experiment looked the charm quarks (c), and their corresponding antiquarks, which have an opposite charge. Image by MissMJ via Wikipedia.

0.8% is small, but significant. How confident are the physicists that their measurements are accurate? Well, the more measurements you take the more confident you can be in your average result, though you can never be 100% certain. The LHC scientists did enough measurements that they could calculate, statistically, that there is only a 0.05% chance that their measurement is wrong.

Beating the Odds: The Sheer Improbability of Being Here

visual.ly posts and hosts some excellent graphics. The one below, calculates the nearly infinitesimal probability of just being born. There’s hardly a better argument for appreciating life.

It’s also a good example of working with probabilities [and] exponents. Very large exponents.

by visually via