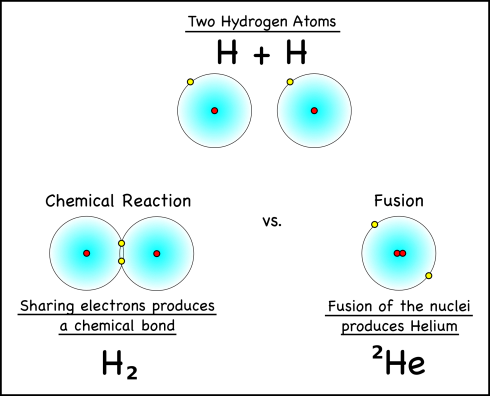
Poetry can be disjointed, illogical and irrational. Sam Tanenhaus argues that that is why poetry helps us make sense of catastrophes and disasters.
One of the enduring paradoxes of great apocalyptic writing is that it consoles even as it alarms.
This has been, in fact, one of the enduring “social” functions of literature — specifically, of poetry. Narrative prose is less well suited to the task. This isn’t surprising: narrative implies continuity and order — events that flow forth in comprehensible sequence, driven by motive forces of cause and effect. …
But catastrophe defies logic. It faces us with disruption and discontinuity, with the breakdown of order. The same can often be said of poetry itself. It operates outside the realm of “logic.” Rather, it obeys the logic of dreams, of the unconscious. This is especially the case with lyric poetry, with its suggestion of vision and prophecy.
— Tanenhaus (2011): The Poetry of Catastrophe, on the New York Times’ Arts Beat Blog.
Andrew Sullivan, on the Daily Dish, highlights W. B. Yeat’s “The Second Coming,” as being quite apt to the topic. It was written just after World War I (Poem of the Week).
Turning and turning in the widening gyre
The falcon cannot hear the falconer;
Things fall apart; the centre cannot hold;
Mere anarchy is loosed upon the world,
The blood-dimmed tide is loosed, and everywhere
The ceremony of innocence is drowned;
The best lack all conviction, while the worst
Are full of passionate intensity.Surely some revelation is at hand;
Surely the Second Coming is at hand.
The Second Coming! Hardly are those words out
When a vast image out of Spiritus Mundi
Troubles my sight: somewhere in sands of the desert
A shape with lion body and the head of a man,
A gaze blank and pitiless as the sun,
Is moving its slow thighs, while all about it
Reel shadows of the indignant desert birds.
The darkness drops again; but now I know
That twenty centuries of stony sleep
Were vexed to nightmare by a rocking cradle,
And what rough beast, its hour come round at last,
Slouches towards Bethlehem to be born?— Yeats (1919): The Second Coming, (via Poets.org).