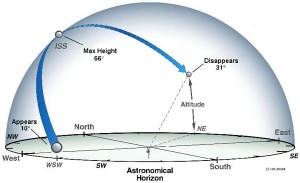
NASA’s Spot the Station website tells you when and where to look to see the space station.
Middle and High School … from a Montessori Point of View
NASA’s Spot the Station website tells you when and where to look to see the space station.

Impressive footage of a storm near Booker Texas, by Mike Olbinski.
Emiland De Cubber‘s excellent instructional on how to make good slideshows.
De Cubber also gives an excellent demonstration of how to fix a terrible slideshow by improving the NSA’s atrocious, leaked slideshow.
More testing of the higher powered stereo-microscope with this flower specimen from a catalpa tree on campus.

The catalpa tree leaf and flower for reference.




In addition to the basic stereoscopes with their fixed 10x and 30x magnifications, we also acquired a zoom stereoscope for more serious research projects. I tried it out with a sprig of lavender blossoms.

The clips on the stage weren’t particularly useful for holding something as small as a single flower, so, to see into the flower, I had to improvise with some of the dissection gear.

At larger magnifications, the focal depth is pretty small so it’s tricky trying to get the big picture. Even thought the camera didn’t quite capture it, you can make out the pollen grains.

I tried slicing the flower longitudinally to get a better look inside, and to see how difficult it would be to identify the major parts.

The photos turned out well using a point-and-shoot Nikon camera through the eyepiece, but even these pictures did not capture all the detail visible to the eye.

With the 2x objective attached, the microscope gets up to 90x magnification, but it becomes very hard clearly see anything after about 60x. All in all, the optics are good, and the lights bright enough to make for a very nice microscope.

A new set of stereo, reflected-light, microscopes came in last week, and I’ve been testing them out. MPU has a good eye for these things, so I asked him to collect some samples for examination.
The first thing he came up with was this beautiful green onion. The seed head has some remarkable colors, and the microscopes are of good enough quality that we could examine in quite good detail at 10x magnification. We were even able to see a few small insects hanging out on the seed head that would have been invisible to the naked eye. They didn’t like the light, however, and hid before I could get a good photo.

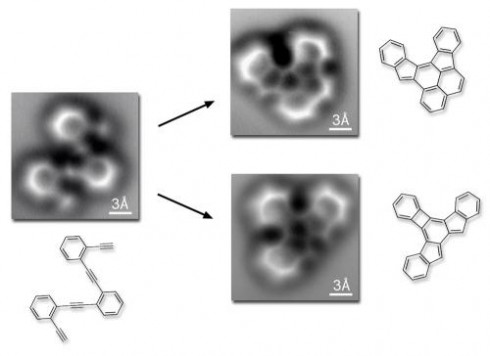
Following closely after the first pictures of atoms we now have pictures of molecules reacting:
Paul Brians’ excellent reference, Common Errors in English Usage, is available online.
An example:
LOSE/LOOSE
This confusion can easily be avoided if you pronounce the word intended aloud. If it has a voiced Z sound, then it’s “lose.” If it has a hissy S sound, then it’s “loose.” Here are examples of correct usage: “He tends to lose his keys.” “She lets her dog run loose.” Note that when “lose” turns into “losing” it loses its “E.”
Brians, 2008. Common Errors in English Usage