So we’re studying graphs (data representation) for math this cycle. Slate Labs has a neat scattergram showing Brett Farve’s vacillating comments about his likelyhood of retierment for the last three years.
Tag: math
Powers of Ten online
The Powers of Ten video, which we use in the lesson on modern exploration is now online.
The Powers of Ten website also has a nice little interactive illustration that shows all the different scales.
Explaining algebra: concrete to abstract
Concrete to abstract, or abstract to concrete? Bottom up or top down? Introducing new concepts can be done either way, but which way is best? Students tend to learn better when they’re building on an existing scaffolding. However, some students are more adept at seeing the bigger picture first then analyzing the details, while others favor seeing the smaller details and constructing the bigger picture of the pieces of the puzzle.
In yesterday’s lesson introducing algebra, I started concretely with weights on the scale for variables and the fulcrum as the equal sign. But I worked with them abstractly. Instead of telling students I had 200 g, 100 g and 50 g weights, I said we had three types of weights and called them a, b and c.
The weights were set on the scales as above so we wrote out the equation:
![]()
and simplified to give:
![]()
Then we talked about balance. Whatever you do to one side you have to do to the other, so I took the c weights off and showed how it solved for a:
![]()
![]()
Now you can solve for b by dividing everything by 2 to get:
![]()
![]()
However, since you can’t exactly divide the 200 g weight into two, you can’t exactly demonstrate this, but at least you can show the math. You can also now substitute in the values for the weights. If b = 100 g.
![]()
![]()
![]()
At this point, students could look at the weights and see the numbers.
Concrete to abstract and back again, I like how the lesson turned out, although, today I had to go over how to show their work again.
And Pythagoras Scores!

Our school, Lamplighter, has started up a couple soccer teams to play in the local under-8 and under-6 leagues this year. I’m now one of the under-6 coaches, and the curious similarities between them and the middle schoolers is going to have to be the topic of another post; Montessori observed some interesting parallels between the first and third planes of development that are worth getting into. However, since the teams are new, we did not have lines on the practice field. And teaching throw-ins is kinda tricky with imaginary lines.
One of the parents/coaches of the under-8 team, Mr. Surbrook, offered draw out the lines. He also volunteered to give a lesson on geometry and let the middle school (and upper elementary) students help.

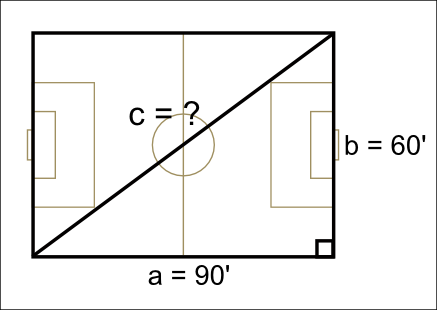
To prepare the middle schoolers I did a quick review of Pythagoras’ Theorem using the 3×3, 4×4 and 5×5 squares (see above).
![]()
The lesson was interesting because the 7th graders had had a more recent exposure to the equation but, unlike the 8th graders, have not had any algebra yet, so there were some puzzled looks when I rearranged the equation.

That was in the morning. After lunch Mr. Surbrook came in and showed us how to use Pythagoras’ Theorem to make right angles and locate the center of the field. If stretch out six pieces of string, four for the sides and two for the diagonals (calculated with the equation,) at their fullest extent you have a rectangle with decent right angles.

After figuring out the theory inside, we went out to the field and help cut the string and lay out the lines. The kids were a bit disappointed they did not get to actually paint the lines, but we’d run out of time for the day.
Fortunately, they’ll get another chance at surveying when Dr. Houghton brings her class out to map the topography of the campus.
I very much liked how the whole procedure went, with my preparatory lesson first, then Mr. Surbrook practical lesson, and finally the actual practical application. We did something similar when we laid out the greenhouse the first time. That time we threw the kids in without a guide and without the practical lesson. It was a bit of a team-building exercise. It also took quite a bit longer.
LaTeX
The easy way to stick mathematical equations into documents would probably be to use Microsoft’s Equation Editor in Word. But that makes it difficult to transfer things from one computer to another, especially if someone does not have MS Word. I prefer to use LaTeX. It’s free, open-source and usually pretty easy to set up on a server. It enables me to put equations inline on the class wiki and now, thanks to the Easy LaTeX plugin I can have them on the blog too.
I’ve been wanting to do this especially since doing the jam algebra post. Then I was lucky that I could, just barely, do everything with text. Now, however, instead of:
(7) 0.4 s / 0.4 = 0.6 j / 0.4
I can do this:
(7) ![]()
Which has it’s pluses and minuses. However, before I would not have been able to do this (at least not very easily):
![]()
Using the LaTeX math markup is not exactly trivial (if you put your cursor over the equation you can see it), but Kocbach (date unknown) and Downes (2002) are great resources.
Pi.z.z.a
To help build up your logical/mathematical intelligence, here is the equation for the volume of a pizza.
Mathematics in the natural world
Mathematics is the language of science. Scientists refine and refine their observations of the complexity of the natural world and try to boil these complex observations down to simple relationships, relationships that are expressed in mathematics. This, I think, is part of the human condition. Our brains are designed to extract simple relationships, heuristics, rules of thumb, from the observations of our senses. It is why Einstein’s equation, E=mc2, has captivated our imagination for so long, why physicists struggle to find the unified theory, and why fractals are so fascinating.
Cristóbal Vila’s short video (found via The Daily Dish) captures some of the magic of the relationship between mathematics and the world.
Statistical significance
A discussion of statistical significance is probably a bit above middle school level, but I’m posting a note here because it is a reminder about the importance of statistics. In fact, students will hear about confidence intervals when they hear about the margin of error of polls in the news and the “significant” benefits of new drugs. Indeed, if you think about it, the development of formal thinking skills during adolescence should make it easier for students to see the world from a more probabilistic perspective, noticing the shades of grey that surround issues, rather that the more black and white, deterministic, point of view young idealists tend to have. At any rate, statistics are important in life but, according to a Science Magazine article, many scientists are not using them correctly.
One key error is in understanding the term “statistically significant”. When Ronald A. Fisher came up with the concept he arbitrarily chose 95% as the cutoff to test if an experiment worked. The arbitrariness is one part of the problem, 95% still means there is one chance in twenty that the experiment failed and with all the scientists conducting experiments, that’s a lot of unrecognized failed experiments.
But the big problem is the fact that people conflate statistical significance and actual significance. Just because there is a statistically significant correlation between eating apples and acne, does not mean that it’s actually important. It could be that this result predicts that one person in ten million will get acne from eating apples, but is that enough reason to stop eating apples?
It is a fascinating article that deals with a number of other erroneous uses of statistics, but I’ve just spent more time on this post than I’d planned (it was supposed to be a short note). So I’d be willing to bet that there is a statistically significant correlation between my interest in an issue and the length of the post (and no correlation with the amount of time I intended to spend on the post).
