Learning Matricies by Programming a Matrix Solver

One of my pre-Calculus students convinced me that the best way for him to learn how to work with matrices was for him to program a matrix solver. I helped him create a Gaussian Elimination solver in Python (which we’ve been using since last year).

Gaussian Elimination Matrix Solver by Alex Shine (comments by me).

from visual import *

'''The coefficient matrix (m) can be any sized square matrix 
   with an additional column for the solution'''
m = [ [1,-2,1,-4],[0,1,2,4],[2,3,-2,2]]

'''Convert the input matrix, m (which is a list) into an array'''
a = array(m,float)
print "Input matrix:"
print a
print

'''Get the shape of the matrix (number of rows and columns)'''
(r,c) = a.shape 

rs = (1-r)

'''Solve'''
for j in range(r):

    print "Column #:", j
    for i in range(r):
        if a[i,j] <> 0:
            a[i,:] = a[i,:] / a[i,j]
    print a
    print

    for i in range(rs+j,j):
        if a[i,j] <> 0:
            a[i,:] = a[j,:] - a[i,:]
    print a
    print

print "Solution"
for i in range (r):
    a[i,:] = a[i,:] / a[i,i]
    print "Variable", i, "=", a[i,-1]

print
print "Solution Matrix:"
print a

The code above solves the following system of equations:


  x - 2y +  z = -4 
       y + 2z =  4 
 2x + 3y - 2z =  2

Which can be written in matrix form as such:

$\left[ \begin{array}{ccc} 1 & -2 & 1 \\ 0 & 1 & 2 \\ 2 & 3 & -2 \end{array} \right] \left[ \begin{array}{c} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{c} -4 \\ 4 \\ 2 \end{array} \right]$

You use the solver by taking the square matrix on the left hand side of the equation and combining it with the column on the hand side as an additional column:

$\left[ \begin{array}{cccc} 1 & -2 & 1 & -4 \\ 0 & 1 & 2 & 4\\ 2 & 3 & -2 & 2\end{array} \right]$

This is entered into the program as the line:

m = [ [1,-2,1,-4],[0,1,2,4],[2,3,-2,2]]

When you run the above program you should get the results:

>>> ================================ RESTART ================================
>>> 
Input matrix:
[[ 1. -2.  1. -4.]
 [ 0.  1.  2.  4.]
 [ 2.  3. -2.  2.]]

Column #: 0
[[ 1.  -2.   1.  -4. ]
 [ 0.   1.   2.   4. ]
 [ 1.   1.5 -1.   1. ]]

[[ 1.  -2.   1.  -4. ]
 [ 0.   1.   2.   4. ]
 [ 0.  -3.5  2.  -5. ]]

Column #: 1
[[-0.5         1.         -0.5         2.        ]
 [ 0.          1.          2.          4.        ]
 [-0.          1.         -0.57142857  1.42857143]]

[[ 0.5         0.          2.5         2.        ]
 [ 0.          1.          2.          4.        ]
 [ 0.          0.          2.57142857  2.57142857]]

Column #: 2
[[ 0.2  0.   1.   0.8]
 [ 0.   0.5  1.   2. ]
 [ 0.   0.   1.   1. ]]

[[-0.2  0.   0.   0.2]
 [ 0.  -0.5  0.  -1. ]
 [ 0.   0.   1.   1. ]]

Solution
Variable 0 = -1.0
Variable 1 = 2.0
Variable 2 = 1.0

Solution Matrix:
[[ 1. -0. -0. -1.]
 [-0.  1. -0.  2.]
 [ 0.  0.  1.  1.]]
>>>

Be aware that:

The code is designed to take any size of matrix.
The matrix you put in can not have any zeros on its diagonal, so some manipulation is often necessary before you can use the code.

Other notes:

The negative zeros (-0) that show up especially in the solution matrix may not look pretty but do not affect the solution.
The code imports the vpython module in the first line but what it really needs is the numpy module, which vpython imports, for the arrays.

The next step is to turn this into a function or a class that can be used in other codes, but it’s already proved useful. My calculus students compared their solutions for the coefficients of a quadratic equation that they had to solve for their carpet friction experiment, which was great because their first answers were wrong.

matrix-1299 — A calculus student uses the matrix solver. Mr. Shine is now trying to convert the solver into an iPhone app.

Draining a Bottle Part 2: Linearizing Equations when you have to

Yesterday we used calculus to find the equation for the height of water in a large plastic water bottle as the water drained out of a small hole in the bottom.

Perhaps the most crucial point in the procedure was fitting a curve to the measured reduction of the water’s outflow rate over time. Yesterday, in our initial attempt, we used a straight line for the curve, which produced a very good fit.

q-v-t — Figure 1. The change in the outflow rate over time can be well approximated by a straight line.

The R² value is a measure of how good a fit the data is to the trendline. The straight line gives an R² value of 0.9854, which is very close to a perfect fit of 1.0 (the lowest R² can go is 0.0).

The resulting equation, written in terms of the outflow rate (dV/dt) and time (t), was:

$\frac{dV}{dt} = -0.0035 t + 3.9113$

However, if you look carefully at the graph in Figure 1, the last few data points suggest that the outflow does not just linearly decrease to zero, but approaches zero asymptotically. As a result, a different type of curve might be a better trendline.

Types of Equations

So my calculus students and I, with a little help from the pre-Calculus class, tried to figure out what types of curves might work. There are quite a few, but we settled for looking at three: a logarithmic function, a reciprocal function, and a square root function. These are shown in Figure 2.

type-curves-300 — Figure 2. Example curves that might better describe the relationship between outflow and time.

I steered them toward the square root function because then we’d end up with something akin to Torricelli’s Law (which can be derived from the physics). A basic square root function for outflow would look something like this:

$\frac{dV}{dt} = a \sqrt{t} + b$

the a coefficient stretches the equation out, while the b coefficient moves the curve up and down.

Fitting the Curve

Having decided on a square-root type function, the next problem was trying to find the actual equation. Previously, we used Excel to find the best fit straight line. However, while Excel can fit log, exponential and power curves, there’s no option for fitting a square-root function to a graph.

To get around this we linearized the square-root function. The equation, after all, looks a lot like the equation of a straight line already, the only difference is the square root of t, so let’s substitute in:

$x = \sqrt{t}$

to get:

$\frac{dV}{dt} = a x + b$

Now we can get Excel to fit a straight line to our data, but we have to plot the square-root of time versus temperature instead of the just time versus temperature. So we take the square root of all of our time measurements:

Time	Square root of time	Outflow rate
t (s)	t^1/2 = x (s^1/2)	dV/dt (ml/s)
0.0	0	3.91
45.5	6.75	3.52
97.8	9.89	2.94
140.9	11.87	3.52
197	14.04	3.21
257	16.05	3.01
315.1	17.75	2.81
380.1	19.50	2.53
452.9	21.28	2.23
529.6	23.01	1.92
620.7	24.91	1.69
742.7	27.25	1.45

We can now plot the outflow rate versus the square root of time (Figure 3).

q-v-sqrt(t) — Figure 3. Linear trend relating the outflow rate to the square root of time. The regression coefficient (R²) of 0.9948 is better than the simply linear trend of outlfow rate versus time (which was 0.9854).

The equation Excel gives (Figure 3), is:

$\frac{dV}{dt} = -0.1395 x + 5.21$

and we can substitute back in for x=t^1/2 to get:

$\frac{dV}{dt} = -0.1395 \sqrt{t} + 5.21$

Getting back to the Equation for Height

Now we can do the same procedure we did before to find the equation for height.

First we substitute in V=πr²h:

$\frac{d(\pi r^2 h}{dt} = -0.1395 \sqrt{t} + 5.21$

Factor out the πr² and move it to the other side of the equation to solve for the rate of change of height:

$\frac{dh}{dt} = \frac{-0.1395}{\pi r^2} \sqrt{t} + \frac{5.21}{\pi r^2}$

Then integrate to find h(t) (remember $\sqrt{t} = t^{1/2}$ ) :

$\int \frac{dh}{dt} dt = \int \left( \frac{-0.1395}{\pi r^2} t^{1/2} + \frac{5.21}{\pi r^2} \right) dt$

gives:

$h = \frac{-0.1395}{(3/2) \pi r^2} t^{3/2} + \frac{5.21}{\pi r^2} t + c$

which might look a bit ugly, but that’s only because I haven’t simplified the fractions. Since the radius (r) is 7.5 cm:

$h = -0.000526 t^{3/2} + 0.029 t + c$

Finally we substitute in the initial value (t=0, h=11) to solve for the coefficient:

$c = 11$

giving the equation:

$h = -0.000526 t^{3/2} + 0.029 t + 11$

Plotting the equations shows that it matches the measured data fairly well, although not quite as well as when we used the previous linear function for outflow.

h-v-t_sqrt — Figure 4. Integrating a square root function for the outflow rate gives a modeled function for the changing height over time that slightly undermatches the measured heights.

Discussion

I’m not sure why the square root function for outflow does not give as good a match of the measurements of height as does the linear function, especially since the former better matches the data (it has a better R² value).

It could be because of the error in the measurements; the gradations on the water bottle were drawn by hand with a sharpie so the error in the height measurements there alone was probably on the order of 2-3 mm. The measurement of the outflow volume in the beaker was also probably off by about 5%.

I suspect, however, that the relatively short time for the experiment (about 15 minutes) may have a large role in determining which model fit better. If we’d run the experiment for longer, so students could measure the long tail as the water height in the bottle got close to the outlet level and the outflow rate really slowed down, then we’d have found a much better match using the square-root function. The linear match of the outflow data produces a quadratic equation when you integrate it. Quadratic equations will drop to a minimum and then rise again, unlike the square-root function which will just continue to sink.

Conclusions

The linearization of the square-root function worked very nicely. It was a great mathematical example even if it did not produce the better result, it was still close enough to be worth it.

The Draining of a Plastic Bottle: Integrating a Physics Experiment into Calculus

Abstract

I punched a small hole (about 1mm radius) in a one gallon plastic bottle and had my students measure the rate at which water drained. Even though the apparatus and measurement technique was fairly rough, we were able to, with a little calculus, determine the equation for the height of the water in the bottle as a function of time.

calculus_jug_1110 — Figure 1. A student uses a stopwatch to measure the outflow rate of water from the plastic bottle.

Introduction

Questions about water draining from a tank are a pretty common in calculus textbooks, but there is a significant difference between seeing the problem written down, and having to figure it out from a physical example. The latter is much more challenging because it does not presuppose any relationships for the change in the height of water with time; students must determine the relationship from the data they collect.

The experimental approach mimics the challenges faced by scientists such as Henry Darcy who first determined the formulas for groundwater flow (Darcy, 1733) almost 300 years ago, not long after the development of modern calculus by Newton and Leibniz (O’Conner and Robertson, 1996).

Procedure

I punched a small hole, about 1mm in radius, in the base of a plastic, one-gallon bottle. I chose this particular type of bottle because the bulk of it was cylindrical in shape.

Students were instructed to figure out how the rate at which water flowed out (outflow rate) changed with time, and how the height of the water (h) in the bottle changed with time. These relationships would allow me to predict the outflow rate at any time, as well as how much water was left in the container at any time.

Data collection:

To measure height versus time, we marked the side of the bottle (within the cylindrical region) in one centimeter increments and recorded the time it took for the water level to drop from one mark to the next. There were a total of 11 marks.
To measure the outflow rate, we intercepted the outflow using a 25 ml beaker (not shown in Figure 2), and measured the time it took to fill to the 25 ml mark.

Results

Time elapsed since last measurement	Height of water in container	Time to fill 25ml beaker
Δt (s)	h (cm)	t_f (s)
0.0	11	6.4
45.5	10	7.1
52.3	9	8.5
43.1	8	7.1
56.1	7	7.8
60.6	6	8.3
57.6	5	8.9
65.0	4	9.9
72.8	3	11.2
76.7	2	13.0
91.1	1	14.8
122.0	0	17.3

Table 1: Outflow rate, water height change with time.

To analyze the data, we calculated the total time (the cumulative sum of the elapsed time since the previous measurement) and the outflow rate. The outflow rate is the change in volume with time:

$\text{outflow rate} = \frac{volume}{time} = \frac{dV}{dt} = \frac{25 ml}{t_f}$

So our data table becomes:

Time	Height of water in container	Outflow rate
t (s)	h (cm)	dV/dt (ml/s)
0.0	11	3.91
45.5	10	3.52
97.8	9	2.94
140.9	8	3.52
197	7	3.21
257	6	3.01
315.1	5	2.81
380.1	4	2.53
452.9	3	2.23
529.6	2	1.92
620.7	1	1.69
742.7	0	1.45

Table 2. Height of water and outflow rate of the bottle.

The graph of the height of the water with time shows a curve, although it is difficult to determine precisely what type of curve. My students started by trying to fit a quadratic equation to it, which should work as we’ll see in a minute.

h-v-t — Figure 3. The decrease in height with time is not a straight line (is non-linear).

The plot of the outflow rate versus time, however, shows a pretty good linear trend. (Note that we do not use the first three datapoints (in Table 2), which we believe are erroneous because we were still sorting out the measuring method.)

Although I’ll note here that the data should ideally be modeled using a square root equation (Torricelli’s Law), that is beyond the present scope of the problem (we’ll try that tomorrow as a follow exercise).

Plotting the data in Excel we could add a linear trendline.

q-v-t — Figure 4. The outflow rate decreases linearly with time.

For the linear trendline, Excel gives the equation:

$y = -0.0035 x + 3.9113$

The y-axis is outflow rate (the change in volume with time), and the x axis is time (t), so the linear equation becomes:

$\frac{dV}{dt} = -0.0035 t + 3.9113$

Notice that this is a differential equation.

To determine the rate of at which the height of water in the container is changing, we need to recognize that the container is cylindrical in shape, and the volume (V) of a cylinder depends on its radius (r) and height (h):

$V = \pi r^2 h$

which can be substituted into differential in the rate equation:

$\frac{d(\pi r^2 h)}{dt} = -0.0035 t + 3.9113$

since π and the radius (r) are constants (since the jug’s shape is a cylinder), they can be pulled out of the differential:

$\pi r^2 \frac{dh}{dt} = -0.0035 t + 3.9113$

Dividing through by πr² solves for the rate of change of height:

$\frac{dh}{dt} = \frac{-0.0035 t + 3.9113}{\pi r^2}$

Isolating the coefficients gives:

$\frac{dh}{dt} = \frac{-0.0035}{\pi r^2} t + \frac{3.9113}{\pi r^2}$

This equation should give the rate at which the height changes with time, however, if you look at it carefully you’ll realize that for the time range we’re using (less than 800 seconds) the value of dh/dt will always be positive. We correct this by recognizing that the outflow rate is a loss of water, so a positive outflow should result in a negative change in height, therefore we rewrite the equation as:

$-\frac{dh}{dt} = \frac{-0.0035}{\pi r^2} t + \frac{3.9113}{\pi r^2}$

which gives:

$\frac{dh}{dt} = \frac{0.0035}{\pi r^2} t - \frac{3.9113}{\pi r^2}$

Now comes the calculus

Now, we can use this rate equation to find the equation for height versus time by integrating with respect to time:

$\int \frac{dh}{dt} dt = \int \left( \frac{0.0035}{\pi r^2} t - \frac{3.9113}{\pi r^2} \right) dt$

to get:

$h = \frac{0.0035}{2 \pi r^2} t^2 - \frac{3.9113}{\pi r^2} t + c$

And all we have to do to the find the constant of integration is substitute in a known point, an initial value. As is often the case, the best point to use is the starting point where t=0 makes the rest of the calculations easier. In our case, when t=0, h=11:

$11 = \frac{0.0035}{2 \pi r^2} (0)^2 - \frac{3.9113}{\pi r^2} (0) + c$

so:

$c = 11$

And our final equation becomes:

$h = \frac{0.0035}{2 \pi r^2} t^2 - \frac{3.9113}{\pi r^2} t + 11$

which is a quadratic equation as my students guessed before we did the calculus.

Does it work?

You will notice that in the math above, we never use the height data in determining equation for height versus time; all the calculations are based on the trendline for the outflow rate versus time.

As a result, we can compare the results of our equation to the actual measurements to see if our calculations are even close. Remarkably, they are.

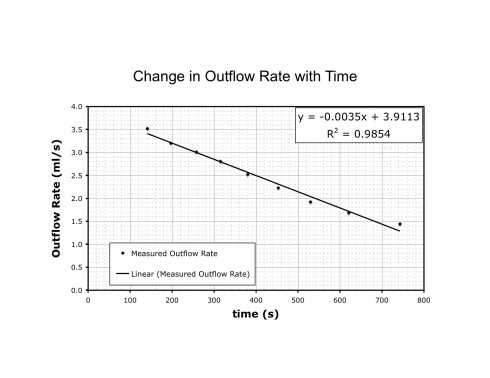
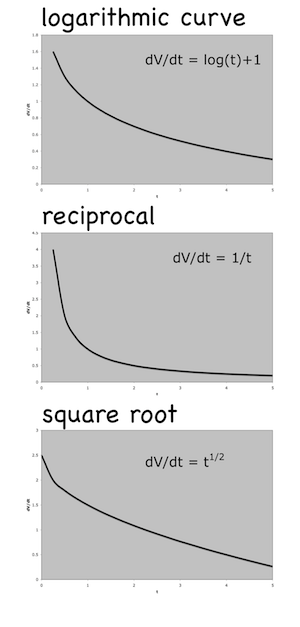
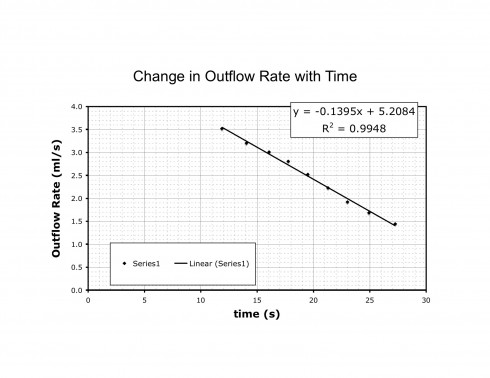
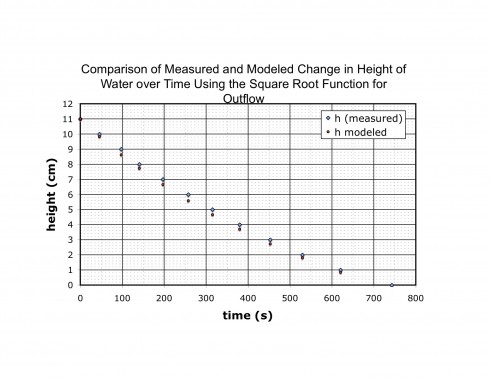
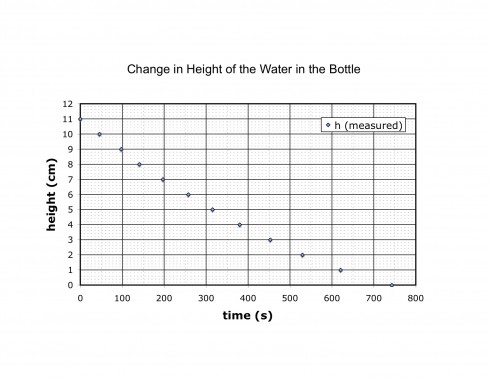
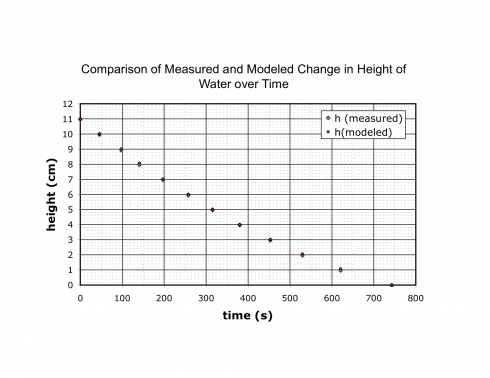
h-v-t-model-v-measured — Figure 5. The results from our equation (modeled) match the measured heights so well, the data points are difficult to distinguish on the graph.

Discussion

Despite all the potential for error, particularly, our relatively crude measurement techniques, and the imperfect cylindrical shape of our plastic bottle, the experiment went remarkably well.

Students found it quite challenging, and required some assistance even though this is a problem they have seen before in their textbook.

The problems in the textbook use Torricelli’s Law, which should much better describe the draining of a tank than the linear equation we find for dV/dt.

Torricelli’s Law:

$\frac{dV}{dt} = a \sqrt{2gh}$

where a is the area of the outlet hole, and g is the acceleration due to gravity.

In our actual experiment it is difficult to tell that a square root function would work better. Excel does not have an option for matching a square root function, so the calculations would become more involved (although it could be set up using Excel’s iterative solver or Goal Seek function).

Conclusion

Our experiment to use calculus to determine the rate of change of the height of water in a leaking plastic water bottle was a successful exercise even though the roughness of the data collection did not permit identification of the square root law for leakage.

What Computer-Based Learning of Math Should Look Like

Walter Russell Mead (and his commenters) highlight two articles (here and here) on Virginia Tech’s excellent computer-based learning setup for their mathematics classes. Most of the work is done on the computer, either at home or in a shared Math Emporium where teachers are available to help when necessary; which, except for the computer work, is very much like how my class works. It seems close to the ideal way of using technology to allow flexibility in learning and assessment, and is in many ways similar to New York City’s School of One program.

VT’s approach requires some self-motivation on the part of the students — students are able to use the 24 hour a day Emporium at any time — but the model should fit be a good fit for Montessori middle and high-school students who have much independence in managing how they use their time during the day.

Their assessment method also nice as it allows students to pace themselves and take their tests when they’re ready. It is based on students proving that they’ve learned the material — how they learned it is not important, nor is how many practice tests they took before they get to the test.

Each course is broken up into a series of “modules,” available on Emporium computers or the Internet, that students are required to complete within a certain amount of time. Each module outlines a specific set of mathematic principles and concepts. These are translated into specific examples to review and problems to solve.

Once the module materials are completed, students can take randomly generated practice tests that draw on a central bank of thousands of potential questions. If they get questions wrong, the computer refers them back to the appropriate materials, and there’s no limit to the number of practice tests they can take. When they decide they’re ready, students come to the Emporium to take an official, proctored test that’s generated in exactly the same way as the practice quizzes. Then they move to the next module. Instead of marking progress by time—the number of hours spent in proximity to a lecturer—Emporium courses measure advancement by evidence of learning.

— Carey, K., 2008: Transformation 101 in Washington Monthly

↬ Tyler Cowen ↬ Walter Russel Mead ↬ Ms. Douglass

Expectations of Math

Jonathan Wai wonders, “Why Is It Socially Acceptable To Be Bad At Math?” After all, it’s not socially acceptable to be illiterate.

The cultural norm that it’s okay to be bad at math has deleterious effects on student motivation. I’ve seen it myself. One parent of an excellent, hard-working student confessed that it was probably her talking about how bad she was at math that helped her kid feel like they didn’t need to work that hard at the subject; especially since the student didn’t think that they were going to use the math anyway.

Some think that the solution is to use a more integrated curriculum and teach, “a math curriculum that focused on real-life problems,”:

Imagine replacing the sequence of algebra, geometry and calculus with a sequence of finance, data and basic engineering. In the finance course, students would learn the exponential function, use formulas in spreadsheets and study the budgets of people, companies and governments. In the data course, students would gather their own data sets and learn how, in fields as diverse as sports and medicine, larger samples give better estimates of averages. In the basic engineering course, students would learn the workings of engines, sound waves, TV signals and computers. Science and math were originally discovered together, and they are best learned together now.

— Garfunkel and Mumford, 2011: How to Fix Our Math Education in the New York Times
— ↬ The Dish ↬ Finding the Next Einstein

Which seems like a good idea — more of an apprenticeship-style approach to math — but there still needs to be some space for the wonderful elegance of some of the apparently more abstract math. More real world applications could certainly be incorporated into the current curriculum, but it would be short-changing our students if we just left math for problem solving and did not delve a little into the principles behind the mathematical techniques they’re using in a more general way.

The Algebra of Straight Lines

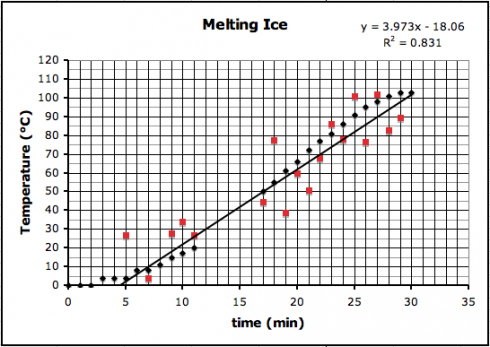
A quick graphical calculator for straight lines — based on This. It’s still incomplete, but it’s functional, and a useful complement to the equation of a straight line animation and the parabola graphing.

You can graph lines based on the equation of a line (in either the slope-intercept or point-slope forms), or from two points.

[inline]

Straight Lines

Slope-Intercept Form	Two Points	Point-Slope Form
`y = m x + b`	`(x₁, y₁) = ( , )`	`y – y₁ = m ( x – x₁)`
y = x +	`(x₂, y₂) = ( , )`	y – = ( x – )

x intercept:	Slope:	Equation:
y intercept:	Points:

[script type=”text/javascript”]

var width=500;
var height=500;
var xrange=10;
var yrange=10;

mx = width/(2.0*xrange);
bx = width/2.0;
my = -height/(2.0*yrange);
by = height/2.0;

document.getElementById(‘testing’).innerHTML = “Hello2”;

function draw_9359(ctx, polys) {

t_9359=t_9359+dt_9359;
//ctx.fillText (“t=”+t, xp(5), yp(5));
ctx.clearRect(0,0,width,height);

polys[0].drawAxes(ctx);
ctx.lineWidth=2;
polys[0].draw(ctx);

polys[0].write_eqn2(ctx);

//ctx.fillText (polys[0].get_parabola_vertex_form_eqn(), xp(5), yp(-5) );

// SHOW 2 POINTS USED TO CALCULATE LINE
if (show_2pts_ctrl_9359.checked==true) {
polys[0].circle_point(ctx, polys[0].p1.x, polys[0].p1.y, “#000”, 0.15);
polys[0].label_point_on_line(ctx, polys[0].p1.x, polys[0].p1.y);
polys[0].circle_point(ctx, polys[0].p2.x, polys[0].p2.y, “#000”, 0.15);
polys[0].label_point_on_line(ctx, polys[0].p2.x, polys[0].p2.y);

}

// SHOW Y INTERCEPT
if (show_y_intercept_ctrl_9359.checked==true) {
polys[0].draw_y_intercept_line(ctx);
document.getElementById(‘y_intercept_pos_9359’).innerHTML = “( 0 , “+ polys_9359[0].c.toPrecision(2)+ ” )”;

if (polys[0].b > 0.0) {
ctx.textAlign=”right”;
xoff = -0.5;
}
else {
ctx.textAlign=”left”;
xoff = 0.5;
}
ctx.fillText (‘y intercept: y = ‘+polys[0].c.toPrecision(2), xp(xoff), yp(polys_9359[0].c+0.25));

} else { document.getElementById(‘y_intercept_pos_9359’).innerHTML = “”;}

// SHOW SLOPE
if (show_slope_ctrl_9359.checked==true) {
polys[0].draw_slope_line(ctx);
document.getElementById(‘slope_pos_9359’).innerHTML = ” = “+polys[0].b.toPrecision(2);

} else { document.getElementById(‘slope_pos_9359’).innerHTML = “”;}

document.getElementById(‘slope_int_equation_9359’).innerHTML = polys[0].get_eqn2();

//SHOW INTERCEPTS
ctx.textAlign=”center”;
if (show_intercepts_ctrl_9359.checked==true) {
polys[0].x_intercepts(ctx);
if (polys[0].order == 2) {
if (polys[0].x_intcpts.length > 0) {
line = “0 = “;
for (var i=0; i 0.0) { sign=”-“;} else {sign=”+”;}
line = line + “(x “+sign+” “+ Math.abs(polys[0].x_intcpts[i].toPrecision(2))+ “)”;
}
ctx.fillText (line, xp(6), yp(7));
for (var i=0; i 0) {
if (polys[0].b > 0.0) {
ctx.textAlign=”right”;
xoff = -0.5;
}
else {
ctx.textAlign=”left”;
xoff = 0.5;
}
ctx.font = “12pt Calibri”;
ctx.fillStyle = “#00f”;
ctx.fillText (‘x intercept: x = ‘+polys[0].x_intcpts[0].toPrecision(2), xp(polys[0].x_intcpts[0]+xoff), yp(0.5));
document.getElementById(‘intercepts_pos_9359’).innerHTML = “( “+ polys[0].x_intcpts[0].toPrecision(2) + “, 0 )”;
}
else {
ctx.fillText (‘None’, xp(7), yp(7));
}

}

}
else {
document.getElementById(‘intercepts_pos_9359’).innerHTML = ” “;
}

// Finding the slope
outln = “

Finding the Slope

“;
outln += “

The slope of the line between the two points is the rise divided by the run: the change in elevation divided by the horizontal distance between the points.”;

// Write out intercept solution
outln = “

Finding the x-intercept

“;
outln += “

Start with the slope-intercept form of the equation:”;
outln += “

“+polys[0].get_eqn2(“y”,”x”,”html”)+”“;
outln += “

Know that at the x-intercept, y = 0 , which you substitute into the equation to get:”;
outln += “

“+polys[0].get_eqn2(“0″,”x”,”html”)+”“;
outln += “

Now move the b coefficient to the other side of the equation:”;
outln += “

“+(-polys[0].c).toPrecision(2)+” = “+ polys[0].b.toPrecision(2)+”x”+”“;
outln += “

And divide both sides by the slope to solve for x:”;
outln += “

“+(-polys[0].c).toPrecision(2)+ ” / “+ polys[0].b.toPrecision(2) + ” = “+ polys[0].b.toPrecision(2)+”x”+ ” / “+ polys[0].b.toPrecision(2)+”“;
outln += “

“+(-polys[0].c/polys[0].b).toPrecision(2)+” = “+”x”+”“;
outln += “

Therefore, the line intercepts the x axis at the point:”;
outln += “

( “+(-polys[0].c/polys[0].b).toPrecision(2)+” , 0 )”;
outln += “

When,”;
outln += “

“+”x = “+ (-polys[0].c/polys[0].b).toPrecision(2) +”“;

document.getElementById(‘x_intercept_9359’).innerHTML = outln;

//Write out the solution by factoring
solution = “

Finding the y-intercept

“;
if (polys[0].order == 2) {
solution = solution + “y = “+polys[0].a.toPrecision(2)+” x² “+polys[0].bsign+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;

solution = solution + ‘Factoring: ‘;

if (polys[0].x_intcpts.length > 0) {
solution = solution + ‘0 = ‘;
for (var i=0; i 0.0) { sign=”-“;} else {sign=”+”;}
solution = solution + “(x “+sign+” “+ Math.abs(polys[0].x_intcpts[i].toPrecision(2))+ “)”;
}
solution = solution + ‘

‘;
solution = solution + ‘Set each factor equal to zero:
‘;
for (var i=0; i 0.0) { sign=”-“;} else {sign=”+”;}
solution = solution + “x “+sign+” “+ Math.abs(polys[0].x_intcpts[i].toPrecision(2))+ ” = 0 “;
}
solution = solution + ‘

and solve for x:
‘;
for (var i=0; i‘;
}
document.getElementById(‘equation_9359’).innerHTML = solution;
}

else if (polys[0].order == 1) {
solution = solution + ‘

At the y-axis x = 0.
To find the y intercept, take the equation of the line, set x = 0, and solve for x.’;
solution = solution + ‘

‘;
solution = solution + “y = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;
solution = solution + ‘ ‘;
solution = solution + ” 0 = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;
solution = solution + ‘ ‘;
solution = solution + (-1.0*polys[0].c).toPrecision(2) +” = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+”

“;
solution = solution + ‘ ‘;
solution = solution + (-1.0*polys[0].c).toPrecision(2)+”/”+polys[0].b.toPrecision(2)+” = “+” x “+”

“;
solution = solution + ‘ ‘;
solution = solution + “x = “+ (-1.0*polys[0].c/polys[0].b).toPrecision(4)+”

“;

document.getElementById(‘equation_9359’).innerHTML = solution;

}

function update_form_9359 () {
b_coeff_9359.value = polys_9359[0].b+””;
c_coeff_9359.value = polys_9359[0].c+””;

y1_coeff_9359.value = polys_9359[0].y1+””;
b1_coeff_9359.value = polys_9359[0].b+””;
x1_coeff_9359.value = polys_9359[0].x1+””;

p1_x_9359.value = polys_9359[0].p1.x+””;
p1_y_9359.value = polys_9359[0].p1.y+””;
p2_x_9359.value = polys_9359[0].p2.x+””;
p2_y_9359.value = polys_9359[0].p2.y+””;
}

//init_mouse();

var c_9359=document.getElementById(“myCanvas_9359”);
var ctx_9359=c_9359.getContext(“2d”);

var change = 0.0001;

function create_lines_9359 () {
//draw line
//document.write(“hello world! “);
var polys = [];
polys.push(addPoly(0,2, 3));
document.getElementById(‘testing’).innerHTML = “Hello”;
polys[0].set_2_points_line();
document.getElementById(‘testing’).innerHTML = “Hello4″;

// polys[1].color = ‘#8C8’;

return polys;
}

var polys_9359 = create_lines_9359();

var x1=xp(-10);
var y1=yp(1);
var x2=xp(10);
var y2=yp(1);
var dc_9359=0.05;

var t_9359 = 0;
var dt_9359 = 100;
//end_ct = 0;
var st_pt_x_9359 = 2;
var st_pt_y_9359 = 1;
var show_y_intercept_9359 = 1; //1 to show y intercept on startup
var show_intercepts_9359 = 0; // 1 to show the intercepts
var show_slope_9359 = 0; // 1 to show the slope
var show_2pts_9359 = 0; // 1 to show the two points from which line can be calculated

var move_dir_9359 = 1.0; // 1 for up

//document.getElementById(‘comment_spot’).innerHTML = polys_9359[0].a+” “+polys_9359[0].b+” “+polys_9359[0].c+” : “+polys_9359[0].h+” “+polys_9359[0].k+” “;

document.getElementById(‘testing’).innerHTML = “Hello3”;

//slope-intercept form
var b_coeff_9359 = document.getElementById(“b_coeff_9359”);
var c_coeff_9359 = document.getElementById(“c_coeff_9359”);

//point-slope form
var y1_coeff_9359 = document.getElementById(“y1_coeff_9359”);
var b1_coeff_9359 = document.getElementById(“b1_coeff_9359”);
var x1_coeff_9359 = document.getElementById(“x1_coeff_9359”);

//equation from two points
var p1_x_9359 = document.getElementById(“x1_9359”);
var p1_y_9359 = document.getElementById(“y1_9359”);
var p2_x_9359 = document.getElementById(“x2_9359”);
var p2_y_9359 = document.getElementById(“y2_9359”);

//options
var show_y_intercept_ctrl_9359 = document.getElementById(“show_y_intercept_9359”);
if (show_y_intercept_9359 == 0) {show_y_intercept_ctrl_9359.checked=false;
} else {show_y_intercept_ctrl_9359.checked=true;}

var show_intercepts_ctrl_9359 = document.getElementById(“show_intercepts_9359”);
if (show_intercepts_9359 == 0) {show_intercepts_ctrl_9359.checked=false;
} else {show_intercepts_ctrl_9359.checked=true;}

var show_slope_ctrl_9359 = document.getElementById(“show_slope_9359”);
if (show_slope_9359 == 0) {show_slope_ctrl_9359.checked=false;
} else {show_slope_ctrl_9359.checked=true;}

var show_2pts_ctrl_9359 = document.getElementById(“show_pts_9359”);
if (show_2pts_9359 == 0) {show_2pts_ctrl_9359.checked=false;
} else {show_2pts_ctrl_9359.checked=true;}

update_form_9359();

//document.write(“test= “+c_coeff_9359.value+” “+polys_9359[0].c);
setInterval(“draw_9359(ctx_9359, polys_9359)”, dt_9359);

b_coeff_9359.onchange = function() {
polys_9359[0].set_b(parseFloat(this.value));
polys_9359[0].update_point_slope_form_line();
polys_9359[0].set_2_points_line();
update_form_9359();
}
c_coeff_9359.onchange = function() {
//polys_9359[0].c = parseFloat(this.value);
polys_9359[0].set_c(parseFloat(this.value));
polys_9359[0].update_point_slope_form_line();
polys_9359[0].set_2_points_line();
update_form_9359();
}

y1_coeff_9359.onchange = function() {
//polys_9359[0].a = parseFloat(this.value);
polys_9359[0].y1 = parseFloat(this.value);
polys_9359[0].update_slope_intercept_form_line();
polys_9359[0].set_2_points_line();
update_form_9359();
}

b1_coeff_9359.onchange = function() {
polys_9359[0].set_b(parseFloat(this.value));
polys_9359[0].update_slope_intercept_form_line();
polys_9359[0].set_2_points_line();
update_form_9359();
}

x1_coeff_9359.onchange = function() {
polys_9359[0].x1 = parseFloat(this.value);
polys_9359[0].update_slope_intercept_form_line();
polys_9359[0].set_2_points_line();
polys_9359[0].set_order()
update_form_9359();
}

p1_x_9359.onchange = function() {
polys_9359[0].p1.x = parseFloat(this.value);
polys_9359[0].update_line_from_2pts();
polys_9359[0].set_order()
update_form_9359();
}

p2_x_9359.onchange = function() {
polys_9359[0].p2.x = parseFloat(this.value);
polys_9359[0].update_line_from_2pts();
polys_9359[0].set_order()
update_form_9359();
}

p1_y_9359.onchange = function() {
polys_9359[0].p1.y = parseFloat(this.value);
polys_9359[0].update_line_from_2pts();
polys_9359[0].set_order()
update_form_9359();
}

p2_y_9359.onchange = function() {
polys_9359[0].p2.y = parseFloat(this.value);
polys_9359[0].update_line_from_2pts();
polys_9359[0].set_order()
update_form_9359();
}

//draw_9359();
//document.write(“x”+x2+”x”);
//ctx_9359.fillText (“n=”, xp(5), yp(5));

[/script]

[/inline]

Curious Correlations

The Correlated website asks people different, apparently unrelated questions every day and mines the data for unexpected patterns.

In general, 72 percent of people are fans of the serial comma. But among those who prefer Tau as the circle constant over Pi, 90 percent are fans of the serial comma.

— ᔥ Correlated.org: March 23’s Correlation.

Two sets of data are said to be correlated when there is a relationship between them: the height of a fall is correlated to the number of bones broken; the temperature of the water is correlated to the amount of time the beaker sits on the hot plate (see here).

snow-T_data-0643 — A positive correlation between the time (x-axis) and the temperature (y-axis).

In fact, if we can come up with a line that matches the trend, we can figure out how good the trend is.

The first thing to try is usually a straight line, using a linear regression, which is pretty easy to do with Excel. I put the data from the graph above into Excel (melting-snow-experiment.xls) and plotted a linear regression for only the highlighted data points that seem to follow a nice, linear trend.

melting-snow-graph-2 — Correlation between temperature (y) and time (x) for the highlighted (red) data points.

You’ll notice on the top right corner of the graph two things: the equation of the line and the R², regression coefficient, that tells how good the correlation is.

The equation of the line is:

y = 4.4945 x – 23.65

which can be used to predict the temperature where the data-points are missing (y is the temperature and x is the time).

You’ll observe that the slope of the line is about 4.5 ºC/min. I had my students draw trendlines by hand, and they came up with slopes between 4.35 and 5, depending on the data points they used.

The regression coefficient tells how well your data line up. The better they line up the better the correlation. A perfect match, with all points on the line, will have a regression coefficient value of 1.0. Our regression coefficient is 0.9939, which is pretty good.

If we introduce a little random error to all the data points, we’d reduce the regression coefficient like this (where R² is now 0.831):

snow-melting-randomized — Adding in some random error causes the data to scatter more, making for a worse correlation. The black dots are the original data, while the red dots include some random error.

The correlation trend lines don’t just have to go up. Some things are negatively correlated — when one goes up the other goes down — such as the relationship between the number of hours spent watching TV and students’ grades.

negative-correlation — The negative correlation between grades and TV watching. Image: ᔥ Lanthier (2002).

Correlation versus Causation

However, just because two things are correlated does not mean that one causes the other.

A jar of water on a hot-plate will see its temperature rise with time because heat is transferred (via conduction) from the hot-plate to the water.

On the other hand, while it might seem reasonable that more TV might take time away from studying, resulting in poorer grades, it might be that students who score poorly are demoralized and so spend more time watching TV; what causes what is unclear — these two things might not be related at all.

Which brings us back to the Correlated.org website. They’re collecting a lot of seemingly random data and just trying to see what things match up.

Curiously, many scientists do this all the time — typically using a technique called multiple regression. Understandably, others are more than a little skeptical. The key problem is that people too easily leap from seeing a correlation to assuming that one thing causes the other.

Everything You (N)ever Wanted to Know About Parabolas

So that my students could more easily check their answers graphically, I put together a page with a more complete analysis of parabolas (click this link for more details).

[inline]

Analyzing Parabolas

Standard Form	Vertex Form
`y = a x² + b x + c`	`y = a (x – h)² + k`
y = x² + x +	y = ( x – ) ² +

Intercepts:	Vertex:
Focus:	Directrix:	Axis:

Solution by Factoring:

y = x² x

[script type=”text/javascript”]
var width=500;
var height=500;
var xrange=10;
var yrange=10;

mx = width/(2.0*xrange);
bx = width/2.0;
my = -height/(2.0*yrange);
by = height/2.0;

function draw_9239(ctx, polys) {
t_9239=t_9239+dt_9239;
//ctx.fillText (“t=”+t, xp(5), yp(5));
ctx.clearRect(0,0,width,height);

polys[0].drawAxes(ctx);
ctx.lineWidth=2;
polys[0].draw(ctx);

polys[0].write_eqn2(ctx);

//polys[0].y_intercepts(ctx);
//write intercepts on graph

// SHOW VERTEX
if (show_vertex_ctrl_9239.checked==true) {
polys[0].draw_vertex(ctx);
document.getElementById(‘vertex_pos_9239’).innerHTML = “(“+polys_9239[0].vertex.x.toPrecision(2)+ ” , “+polys_9239[0].vertex.y.toPrecision(2)+ ” )”;
} else { document.getElementById(‘vertex_pos_9239’).innerHTML = “”;}

// SHOW FOCUS
if (show_focus_ctrl_9239.checked==true) {
polys[0].draw_focus(ctx);
document.getElementById(‘focus_pos_9239’).innerHTML = “(“+polys_9239[0].focus.x.toPrecision(2)+ ” , “+polys_9239[0].focus.y.toPrecision(2)+ ” )”;
} else { document.getElementById(‘focus_pos_9239’).innerHTML = “”;}

// SHOW DIRECTRIX
if (show_directrix_ctrl_9239.checked==true) {
polys[0].draw_directrix(ctx);
document.getElementById(‘directrix_pos_9239’).innerHTML = polys[0].directrix.get_eqn2(“y”,”x”,”html”);

polys[0].directrix.write_eqn2(ctx, polys[0].directrix.get_eqn2(“directrix: y”));
} else { document.getElementById(‘directrix_pos_9239’).innerHTML = “”;}

// SHOW AXIS
if (show_axis_ctrl_9239.checked==true) {
polys[0].draw_parabola_axis(ctx);
document.getElementById(‘axis_pos_9239’).innerHTML = “x = “+polys[0].vertex.x.toPrecision(2);
}

//SHOW INTERCEPTS
ctx.textAlign=”center”;
if (show_intercepts_ctrl_9239.checked==true) {
polys[0].x_intercepts(ctx);
ctx.fillText (‘x intercepts: (when y=0)’, xp(6), yp(8));
//ctx.fillText (‘intercepts=’+polys[0].x_intcpts.length, xp(5), yp(-5));
if (polys[0].order == 2) {
if (polys[0].x_intcpts.length > 0) {
line = “0 = “;
for (var i=0; i 0.0) { sign=”-“;} else {sign=”+”;}
line = line + “(x “+sign+” “+ Math.abs(polys[0].x_intcpts[i].toPrecision(2))+ “)”;
}
ctx.fillText (line, xp(6), yp(7));
for (var i=0; i 0) {
for (var i=0; i2 “+polys[0].bsign+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;

solution = solution + ‘Factoring: ‘;

and solve for x:
‘;
for (var i=0; i‘;
}
document.getElementById(‘equation_9239’).innerHTML = solution;
}

else if (polys[0].order == 1) {
solution = solution + ‘
‘;
solution = solution + “y = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;
solution = solution + ‘

Set y=0 and solve for x:
‘;
solution = solution + ” 0 = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+ polys[0].csign+” “+Math.abs(polys[0].c.toPrecision(2))+”

“;
solution = solution + ‘ ‘;
solution = solution + (-1.0*polys[0].c).toPrecision(2) +” = “+” “+Math.abs(polys[0].b.toPrecision(2))+” x “+”

“;
solution = solution + ‘ ‘;
solution = solution + (-1.0*polys[0].c).toPrecision(2)+”/”+polys[0].b.toPrecision(2)+” = “+” x “+”

“;
solution = solution + ‘ ‘;
solution = solution + “x = “+ (-1.0*polys[0].c/polys[0].b).toPrecision(4)+”

“;

document.getElementById(‘equation_9239’).innerHTML = solution;
}

}

function update_form_9239 () {
a_coeff_9239.value = polys_9239[0].a+””;
b_coeff_9239.value = polys_9239[0].b+””;
c_coeff_9239.value = polys_9239[0].c+””;

av_coeff_9239.value = polys_9239[0].a+””;
hv_coeff_9239.value = polys_9239[0].h+””;
kv_coeff_9239.value = polys_9239[0].k+””;

}

//init_mouse();

var c_9239=document.getElementById(“myCanvas_9239”);
var ctx_9239=c_9239.getContext(“2d”);

var change = 0.0001;

function create_lines_9239 () {
//draw line
//document.write(“hello world! “);
var polys = [];
polys.push(addPoly(1,6, 5));

// polys.push(addPoly(0.25, 1, 0));
// polys[1].color = ‘#8C8’;

return polys;
}

var polys_9239 = create_lines_9239();

var x1=xp(-10);
var y1=yp(1);
var x2=xp(10);
var y2=yp(1);
var dc_9239=0.05;

var t_9239 = 0;
var dt_9239 = 100;
//end_ct = 0;
var st_pt_x_9239 = 2;
var st_pt_y_9239 = 1;
var show_vertex_9239 = 1; //1 to show vertex on startup
var show_focus_9239 = 1; // 1 to show the focus
var show_intercepts_9239 = 1; // 1 to show the intercepts
var show_directrix_9239 = 1; // 1 to show the directrix
var show_axis_9239 = 1; //1 to show the axis of the parabola

var move_dir_9239 = 1.0; // 1 for up

//document.getElementById(‘comment_spot’).innerHTML = polys_9239[0].a+” “+polys_9239[0].b+” “+polys_9239[0].c+” : “+polys_9239[0].h+” “+polys_9239[0].k+” “;

//standard form
var a_coeff_9239 = document.getElementById(“a_coeff_9239”);
var b_coeff_9239 = document.getElementById(“b_coeff_9239”);
var c_coeff_9239 = document.getElementById(“c_coeff_9239”);

//vertex form
var av_coeff_9239 = document.getElementById(“av_coeff_9239”);
var hv_coeff_9239 = document.getElementById(“hv_coeff_9239”);
var kv_coeff_9239 = document.getElementById(“kv_coeff_9239”);

//options
var show_vertex_ctrl_9239 = document.getElementById(“show_vertex_9239”);
if (show_vertex_9239 == 0) {show_vertex_ctrl_9239.checked=false;
} else {show_vertex_ctrl_9239.checked=true;}

var show_focus_ctrl_9239 = document.getElementById(“show_focus_9239”);
if (show_focus_9239 == 0) {show_focus_ctrl_9239.checked=false;
} else {show_focus_ctrl_9239.checked=true;}

var show_intercepts_ctrl_9239 = document.getElementById(“show_intercepts_9239”);
if (show_intercepts_9239 == 0) {show_intercepts_ctrl_9239.checked=false;
} else {show_intercepts_ctrl_9239.checked=true;}

var show_directrix_ctrl_9239 = document.getElementById(“show_directrix_9239”);
if (show_directrix_9239 == 0) {show_directrix_ctrl_9239.checked=false;
} else {show_directrix_ctrl_9239.checked=true;}

var show_axis_ctrl_9239 = document.getElementById(“show_axis_9239”);
if (show_axis_9239 == 0) {show_axis_ctrl_9239.checked=false;
} else {show_axis_ctrl_9239.checked=true;}

update_form_9239();

//document.write(“test= “+c_coeff_9239.value+” “+polys_9239[0].c);
setInterval(“draw_9239(ctx_9239, polys_9239)”, dt_9239);

a_coeff_9239.onchange = function() {
//polys_9239[0].a = parseFloat(this.value);
polys_9239[0].set_a(parseFloat(this.value));
polys_9239[0].update_vertex_form_parabola();
update_form_9239();
}
b_coeff_9239.onchange = function() {
//polys_9239[0].b = parseFloat(this.value);
polys_9239[0].set_b(parseFloat(this.value));
polys_9239[0].update_vertex_form_parabola();
update_form_9239();
}
c_coeff_9239.onchange = function() {
//polys_9239[0].c = parseFloat(this.value);
polys_9239[0].set_c(parseFloat(this.value));
polys_9239[0].update_vertex_form_parabola();
update_form_9239();
}

av_coeff_9239.onchange = function() {
//polys_9239[0].a = parseFloat(this.value);
polys_9239[0].set_a(parseFloat(this.value));
polys_9239[0].update_standard_form_parabola();
update_form_9239();
}

hv_coeff_9239.onchange = function() {
polys_9239[0].h = parseFloat(this.value);
polys_9239[0].update_standard_form_parabola();
polys_9239[0].set_order()
update_form_9239();
}

kv_coeff_9239.onchange = function() {
polys_9239[0].k = parseFloat(this.value);
polys_9239[0].update_standard_form_parabola();
polys_9239[0].set_order()
update_form_9239();
}

//draw_9239();
//document.write(“x”+x2+”x”);
//ctx_9239.fillText (“n=”, xp(5), yp(5));

[/script]

[/inline]

Converting the forms

The key relationships are the ones to convert from the standard form of the parabolic equation:

$y = a x^2 + b x + c$

(1)

to the vertex form:

$y = a (x - h)^2 + k$

(2)

If you multiply out the vertex equation form you get:

y = a x² – 2ah x + ah² + k

(3)

When you compare this equation to the standard form of the equation (Equation 1), if you look at the coefficients and the constants, you can see that:

To convert from the vertex to the standard form use:

         $a = a$ (4)

         $b = -2ah$ (5)

         $c = ah^2 + k$ (6)

Going the other way,

To convert from the standard to the vertex form of parabolic equations use:

         $a = a$
(7)

         $h = \frac{-b}{2a}$
(8)

         $k = c - ah^2$
(9)

Although it is sometimes convenient to let k not depend on coefficients from its own equation:

$k = c - \frac{b^2}{4a}$ (10)

The Vertex and the Axis

The nice thing about the vertex form of the equation of the parabola is that if you want the find the coordinates of the vertex of the parabola, they’re right there in the equation.

Specifically, the vertex is located at the point:

$(x_v, y_v) = (h, k)$

(11)

The axis of the parabola is the vertical line going through the vertex, so:

The equation for the axis of a parabola is:

$x = h$

(12)

Focus and Directrix

Finally, it’s important to note that the distance (d) from the vertex of the parabola to its focus is given by:

$d = \frac{1}{4a}$

(13)

Which you can just add d on to the coordinates of the vertex (Equation 11) to get the location of the focus.

$(x_f, y_f) = (x_v, y_v + d)$

(14)

The directrix is just the opposite, vertical distance away, so the equation for the directrix is the equation of the horizontal line at:

$y = y_v + d$

(15)

References

There are already some excellent parabola references out there including:

Wonderful interactive graphs by Murray Bourne.
Nice simple explanations of the different forms of the equations.
More complex explanations from Wolfram Alpha.