Tag: math

Quick Reference: Adding Fractions with Different Denominators

To add fractions with different denominators you just need to multiply each fraction to get the same denominator:

Take:
\frac{3}{5} + \frac{5}{9}

The easiest common denominator will be the product of both denominators ( 5 × 9 = 45 ). So multiply each fraction.

\frac{3}{5}\times\frac{9}{9} + \frac{5}{9} \times\frac{5}{5}

Notice that you’re really multiplying each fraction by 1 (since 9/9 = 1 and 5/5 = 1) and anything multiplied by one remains the same number. So you’re not changing the value of the fraction, just how it looks.

Now doing the multiplication gives:
\frac{3}{5}\times\frac{9}{9} + \frac{5}{9} \times\frac{5}{5} = \frac{27}{45} + \frac{25}{45}

Which we can add because we now have a common denominator:
\frac{27}{45} + \frac{25}{45} = \frac{52}{45}

And simplify to give a mixed number:
\frac{52}{45} = 1\frac{7}{45}

Reasons to Study Algebra: Economics


I hope you think that I am an acceptable writer, but when it comes to economics I speak English as a second language: I think in equations and diagrams, then translate.

— Krugman (1996): Economic Culture Wars in Slate

I sometimes get the question: Why do I have to learn algebra? Followed by the statement: I’m never going to have to use it again. My response is that it’s a bit like learning to read; you can survive in society being illiterate, but it’s not easy. The same goes for algebra, but it’s a little more complex.

Paul Krugman argues for the importance of algebra for anyone thinking about economics, the economy, and what to do about it. Even at the basic level, economists think in mathematical equations and algebraic models, then they have to translate their thoughts into English to communicate them. People who are not familiar with algebra are at a distinct advantage.

There are important ideas … that can be expressed in plain English, and there are plenty of fools doing fancy mathematical models. But there are also important ideas that are crystal clear if you can stand algebra, and very difficult to grasp if you can’t. [my emphasis] International trade in particular happens to be a subject in which a page or two of algebra and diagrams is worth 10 volumes of mere words. That is why it is the particular subfield of economics in which the views of those who understand the subject and those who do not diverge most sharply.

— Krugman (1996): Economic Culture Wars in Slate

P.S. In the article, he also points out the importance of algebra in the field of evolutionary biology.

Serious evolutionary theorists such as John Maynard Smith or William Hamilton, like serious economists, think largely in terms of mathematical models. Indeed, the introduction to Maynard Smith’s classic tract Evolutionary Genetics flatly declares, “If you can’t stand algebra, stay away from evolutionary biology.” There is a core set of crucial ideas in his subject that, because they involve the interaction of several different factors, can only be clearly understood by someone willing to sit still for a bit of math.

↬ Reddit

Teaching Math Backwards

Having just had the chance to teach the entire upper (secondary) school math curriculum, I’ve been doing a little bit of necessary reflection on how to help students get interested. One of the key things we learned in the Montessori training was just how much more students learn when they’re self-motivated about a topic.

The common theme among all these classes was the use of the math to construct models to better understand the relationships between different things.

Figure 1. The rising temperatures in the middle of the graph can be modeled with a straight line. Graph by A.F.

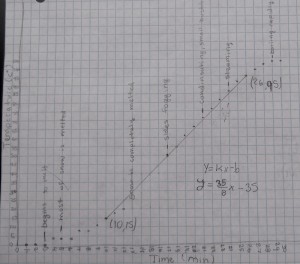
In Algebra I the focus is on linear models, like the one my middle schoolers drew from the results of their ice-melting experiment in science (see Figure 1). Another example (that I’ve not posted on yet) is calculating the density of liquids from a graph of volume and mass.

By the time they get to calculus they’re not just dealing with more complex functions, but they’re integrating and differentiating them to derive fundamental relationships.

Linearized graph of outflow rate versus the square root of time. From the draining water experiment.

h = \int \frac{dh}{dt} dt = \int \left( \frac{-0.1395}{\pi r^2} t^{1/2} + \frac{5.21}{\pi r^2} \right) dt

Unfortunately, you usually end up with useful applications at the end of the book (or the chapter).

I wonder if it would not be more effective to put the examples in at the beginning. Not just in a little box for, “Why this is useful,” but start with the problem and then introduce the math need to solve it. A bit, perhaps, like Garfunkel and Mumford’s op-ed suggestion for more “real-life problems” in math education.

Momentum

A ball rolling down a ramp hits a car which moves off uphill. Can you come up with an experiment to predict how far the car will move if the ball is released from any height? What if different masses of balls are used?

Students try to figure out the relationship between the ball's release height and how far the car moves.

For my middle school class, who’ve been dealing with linear relationships all year, they could do this easily if the distance the car moves is directly proportional to height from which the ball was released?

The question ultimately comes down to momentum, but I really didn’t know if the experiment would work out to be a nice linear relationship. If you do the math, you’ll find that release height and the maximum distance the car moves are directly proportional if the momentum transferred to the car by the ball is also directly proportional to the velocity at impact. Given that wooden ball and hard plastic car would probably have a very elastic collision I figured there would be a good chance that this would be the case and the experiment would work.

It worked did well enough. Not perfectly, but well enough.

Music of the Fibonacci Sequence

Tool‘s Lateralus has the Fibonacci Sequence embedded into it. Ms. Wilson tells me that some of her Algebra II students were able to detect it out after listening to the song (a few times), but this video has the highlights where the sequence occurs.

↬ Ms. Wilson