An interesting application of statistical thinking used to estimate the number of tanks Germany was producing during WW2.
Tag: statistics
Comparing Covid Cases of US States
Based on my students’ statistics projects, I automated the method (using R) to calculate the z-score for all the states in the U.S. We used the John Hopkins daily data.
I put graphs for all of the states on the COVID: The U.S. States Compared webpage.
The R functions (test.R) assumes all of the data is in a folder (COVID-19-master/csse_covid_19_data/csse_covid_19_daily_reports_us/), and outputs the graphs to the folder ‘images/zscore/‘ which needs to exist.
covid_data <- function(infile, state="Missouri") {
filename <- paste(file_dir, infile, sep='')
mydata <- read.csv(filename)
pop <- read.csv('state_populations.txt')
mydata <- merge(mydata, pop)
mydata$ConfirmedPerCapita1000 <- mydata$Confirmed / mydata$Population *1000
summary(mydata$ConfirmedPerCapita1000)
stddev <- sd(mydata$ConfirmedPerCapita1000)
avg <- mean(mydata$ConfirmedPerCapita1000)
cpc1k <- mydata[mydata$Province_State == state,]$ConfirmedPerCapita1000
zscore <- (cpc1k - avg)/stddev
#print(infile, zscore)
return(zscore)
}
get_zScore_history <-function(state='Missouri') {
df <- data.frame(Date=as.Date(character()), zscore=numeric())
for (f in datafiles){
dateString <- as.Date(substring(f, 1, 10), format='%m-%d-%y')
zscore <- covid_data(f, state=state)
df[nrow(df) + 1,] = list(dateString, zscore)
}
df$day <- 1:nrow(df)
plot_zScore(df, state)
# LINEAR REGRESSIONS:
# http://r-statistics.co/Linear-Regression.html
lmod <- lm(day ~ zscore, df)
return(df)
}
plot_zScore <- function(df, state){
max_z <- max( abs(max(df$zscore)), abs(min(df$zscore)))
print(max_z)
zplot <- plot(x=df$day, y=df$zscore, main=paste('z-score: ', state), xlab="Day since April 20th, 2020", ylab='z-score', ylim=c(-max_z,max_z))
abline(0,0, col='firebrick')
dev.copy(png, paste('images/zscore/', state, '-zscore.png', sep=''))
dev.off()
}
get_states <- function(){
lastfile <- datafiles[ length(datafiles) ]
filename <- paste(file_dir, lastfile, sep='')
mydata <- read.csv(filename)
pop <- read.csv('state_populations.txt')
mydata <- merge(mydata, pop)
return(mydata$Province_State)
}
graph_all_states <- function(){
states <- get_states()
for (state in states) {
get_zScore_history(state)
}
}
file_dir <- 'COVID-19-master/csse_covid_19_data/csse_covid_19_daily_reports_us/'
datafiles <- list.files(file_dir, pattern="*.csv")
print("To get the historical z-score data for a state run (for example):")
print(" > get_zScore_history('New York')" )
df = get_zScore_history()
You can run the code in test.R in the R console using the commands:
> source('test.R')which does Missouri by default, but to do other states use:
> get_zScore_history('New York')To get all the states use:
> graph_all_states()Basic R (using Covid data)
Once you start R you’ll need to figure out which directory you’re working in:
> getwd()On a Windows machine your default working directory might be something like:
[1] "C:/Users/username"On OSX or Linux you’ll get something like:
[1] "/Users/username" To get to the directory you want to work in use setwd(). I’ve put my files into the directory: “/Users/lurba/Documents/TFS/Stats/COVID”
To get there from the working directory above I could enter the full path above, or just the relative path like:
> setwd("TFS/Stats/COVID")Now my data is in the file named “04-20-2020.csv” (from the John Hopkins Covid data repository on github) which I’ll read in with:
> mydata <- read.csv("04-20-2020.csv")This creates a variable named “mydata” that has the information in it. I can see the column names by using:
> colnames(mydata)which gives:
[1] "Province_State" "Country_Region" "Last_Update"
[4] "Lat" "Long_" "Confirmed"
[7] "Deaths" "Recovered" "Active"
[10] "FIPS" "Incident_Rate" "People_Tested"
[13] "People_Hospitalized" "Mortality_Rate" "UID"
[16] "ISO3" "Testing_Rate" "Hospitalization_Rate"Let’s take a look at the summary statistics for the number of confirmed cases, which is in the column labeled “Confirmed”:
> summary(mydata$Confirmed) Min. 1st Qu. Median Mean 3rd Qu. Max.
317 1964 4499 15347 13302 253060 This shows that the mean is 15, 347 and the maximum is 253,060 confirmed cases.
I’m curious about which state has that large number of cases, so I’m going to print out the columns with the state names (“Province_State”) and the number of confirmed cases (“Confirmed”). From our colnames command above we can see that “Province_State” is column 1, and “Confirmed” is column 6, so we’ll use the command:
> mydata[ c(1,6) ]The “c(1,6)” says that we want the columns 1 and 6. This command outputs
Province_State Confirmed
1 Alabama 5079
2 Alaska 321
3 American Samoa 0
4 Arizona 5068
5 Arkansas 1973
6 California 33686
7 Colorado 9730
8 Connecticut 19815
9 Delaware 2745
10 Diamond Princess 49
11 District of Columbia 2927
12 Florida 27059
13 Georgia 19407
14 Grand Princess 103
15 Guam 136
16 Hawaii 584
17 Idaho 1672
18 Illinois 31513
19 Indiana 11688
20 Iowa 3159
21 Kansas 2048
22 Kentucky 3050
23 Louisiana 24523
24 Maine 875
25 Maryland 13684
26 Massachusetts 38077
27 Michigan 32000
28 Minnesota 2470
29 Mississippi 4512
30 Missouri 5890
31 Montana 433
32 Nebraska 1648
33 Nevada 3830
34 New Hampshire 1447
35 New Jersey 88722
36 New Mexico 1971
37 New York 253060
38 North Carolina 6895
39 North Dakota 627
40 Northern Mariana Islands 14
41 Ohio 12919
42 Oklahoma 2680
43 Oregon 1957
44 Pennsylvania 33914
45 Puerto Rico 1252
46 Rhode Island 5090
47 South Carolina 4446
48 South Dakota 1685
49 Tennessee 7238
50 Texas 19751
51 Utah 3213
52 Vermont 816
53 Virgin Islands 53
54 Virginia 8990
55 Washington 12114
56 West Virginia 902
57 Wisconsin 4499
58 Wyoming 317
59 Recovered 0
Looking through, we can see that New York was the state with the largest number of cases.
Note that we could have searched for the row with the maximum number of Confirmed cases using the command:
> d2[which.max(d2$Confirmed),]Merging Datasets
In class, we’ve been editing the original data file to add a column with the state populations (called “Population”). I have this in a separate file called “state_populations.txt” (which is also a comma separated variable file, .csv, even if not so labeled). So I’m going to import the population data:
> pop <- read.csv("state_population.txt")Now I’ll merge the two datasets to add the population data to “mydata”.
> mydata <- merge(mydata, pop)Graphing (Histograms and Boxplots)
With the datasets together we can try doing a histogram of the confirmed cases. Note that there is a column labeled “Confirmed” in the mydata dataset, which we’ll address as “mydata$Confirmed”:
> hist(mydata$Confirmed)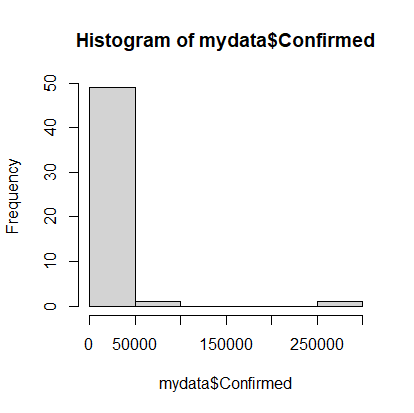
Note that on April 20th, most states had very few cases, but there were a couple with a lot of cases. It would be nice to see the data that’s clumped in the 0-50000 range broken into more bins, so we’ll add an optional argument to the hist command. The option is called breaks and we’ll request 20 breaks.
> hist(mydata$Confirmed, breaks=20)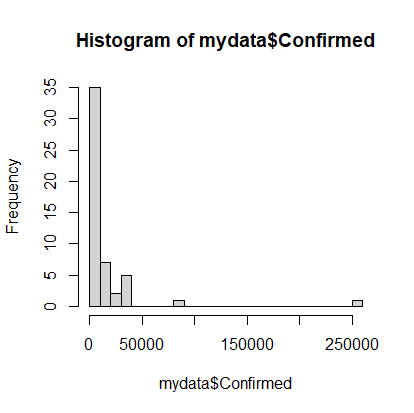
Calculations (cases per 1000 population)
Of course, simply looking at the number of cases in not very informative because you’d expect, with all things being even, that states with the highest populations would have the highest number of cases. So let’s calculate the number of cases per capita. We’ll multiply that number by 1000 to make it more human readable:
> mydata$ConfirmedPerCapita1000 <- mydata$Confirmed / mydata$Population * 1000Now our histogram would look like:
> hist(mydata$ConfirmedPerCapita1000, breaks=20)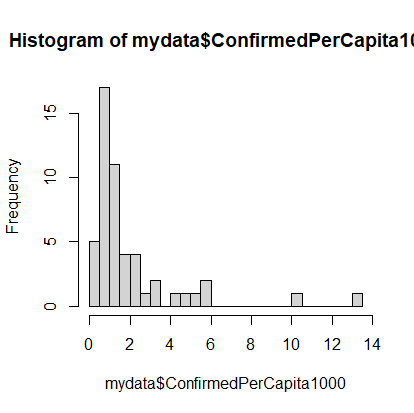
The dataset still has a long tail, but we can see the beginnings of a normal distribution.
The next thing we can do is make a boxplot of our cases per 1000 people. I’m going to set the range option to zero so that the plot has the long tails:
> boxplot(mydata$ConfirmedPerCapita1000, range=0)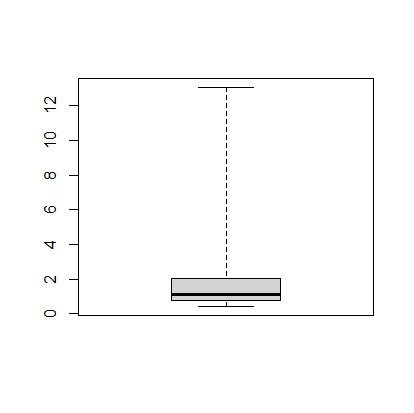
The boxplot shows, more or less, the same information in the histogram.
Finding Specific Data in the Dataset
We’d like to figure out how Missouri is doing compared to the rest of the states, so we’ll calculate the z-score, which tells how many standard deviations you are away from the mean. While there is a built in z-score function in R, we’ll first see how we can use the search and statistics methods to find the relevant information.
First, finding Missouri’s number of confirmed cases. To find all of the data in the row for Missouri we can use:
> mydata[mydata$Province_State == "Missouri",]which gives something like this. It has all of the data but is not easy to read.
Province_State Population Country_Region Last_Update Lat
26 Missouri 5988927 US 2020-04-20 23:36:47 38.4561
Long_ Confirmed Deaths Recovered Active FIPS Incident_Rate People_Tested
26 -92.2884 5890 200 NA 5690 29 100.5213 56013
People_Hospitalized Mortality_Rate UID ISO3 Testing_Rate
26 873 3.395586 84000029 USA 955.942
Hospitalization_Rate ConfirmedPerCapita1000
26 14.82173 0.9834817To extract just the “Confirmed” cases, we’ll add that to our command like so:
> mydata[mydata$Province_State == "Missouri",]$Confirmed[1] 5890Which just gives the number 5890. Or the “ConfirmedPerCapita1000”:
> mydata[mydata$Province_State == "Missouri",]$ConfirmedPerCapita1000
[1] 0.9834817This method would also be useful later on if we want to automate things.
z-score
We have the mean from when we did the summary command, but there’s also a mean command.
> mean(mydata$ConfirmedPerCapita1000)
[1] 2.006805Similarly you can get the standard deviation with the sd function.
> sd(mydata$ConfirmedPerCapita1000)
[1] 2.400277We can now calculate the z-score for Missouri:
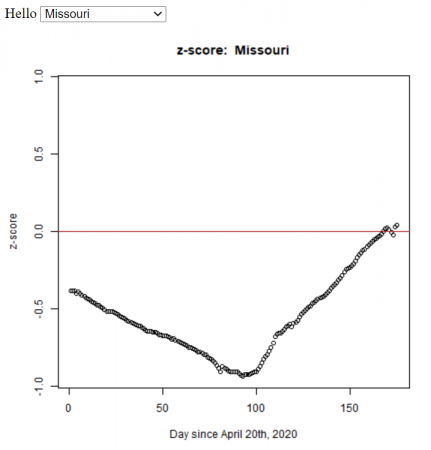
![]()
which gives a results of:
![]()
So it looks like Missouri was doing reasonable well back in April, at least compared to the rest of the country.
How to make a Boxplot in R
Guest post by Grace Appell.
What is a Boxplot?
A box plot is a graph that helps you to analyze a set of data. It used to show the spread of the data. In it you use five data points: the minimum, the 1st quartile, the median, the 3rd quartile, and the maximum.
The minimum is the lowest point in your data set, and the maximum is the largest. The median is the number in the middle of the data set when you have the number lined up numerically.
For example if your data set was this:
5, 6 ,11, 18, 12, 9, 4
First you would put them in order lowest to highest.
4, 5, 6, 9, 11, 12, 18
Your median would be 9, because it is the middle number. The minimum would be 4, and the maximum would be 18.
The first quartile would be 5, the median of the numbers below 9, and the third quartile would be 12, the median of the numbers above 9.
So the data you would use in your boxplot would be
(4,5,9,12,18)
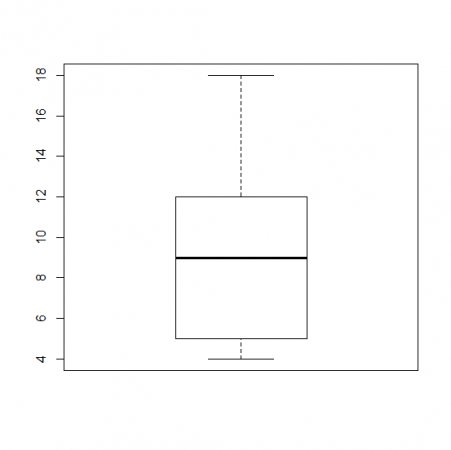
The boxplot would look like would look like this.
What is R?
R is a software program that is free to download that you can use for calculating statistics and creating graphics.
Here is their website: https://www.r-project.org/
Boxplots in R
In R you can create a boxplot by using this formula.
> Name of data set <- c(minimum, quartile 1, median, quartile 3, maximum) > boxplot(Name of data set)
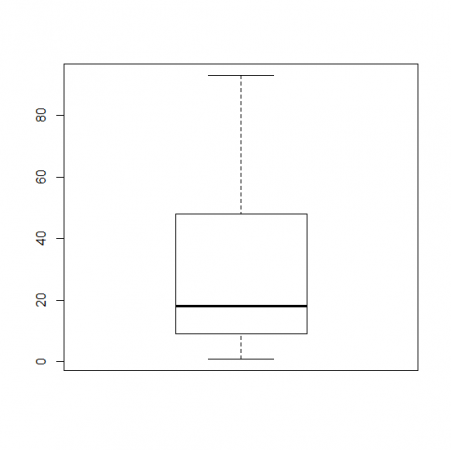
First you have to name your data set. In our project where we analyzed the number of times people repeated their Shakespeare lines that they performed, I used the name Macbeth. So the formula looked like this:
> Macbeth <- c(1,9,18,48,93) > boxplot(Macbeth)
Using this data set, your box plot should look like this
Looking Behind the Statistics
For my statistics students, as we approach the end of the course, to think about the power of statistics and how using them, even with the best intentions, can go wrong.
https://www.npr.org/podcasts/510298/ted-radio-hour: Go to JANUARY 26, 2018. Can We Trust The Numbers?
Getting Data into R
One of my students is taking an advanced statistics course–mostly online–and it introduced her to the statistical package R. I’ve been meaning to learn how to use R for a while, so I had her show me how use it. This allowed me to give her a final exam that used some PEW survey data for analysis. (I used the data for the 2013 LGBT survey). These are my notes on getting the PEW data, which is in SPSS format, into R.
Instructions on Getting PEW data into R
Go to the link for the 2013 LGBT survey“>2013 LGBT survey and download the data (you will have to set up an account if you have not used their website before).
- There should be two files.
- The .sav file contains the data (in SPSS format)
- The .docx file contains the metadata (what is metadata?).
- Load the data into R.
- To load this data type you will need to let R know that you are importing a foreign data type, so execute the command:
> library(foreign)
> file.choose()
> dataset = read.spss(“C:\\Users\...”)
> summary(dataset)
> hist(dataset$Q35)
> write.csv(dataset$Q39, ”helloQ39Data.csv”)
This should be enough to get started with R. One problem we encountered was that the R version on Windows was able to produce the histogram of the dataset, while the Mac version was not. I have not had time to look into why, but my guess is that the Windows version is able to screen out the non-numeric values in the dataset while the Mac version is not. But that’s just a guess.
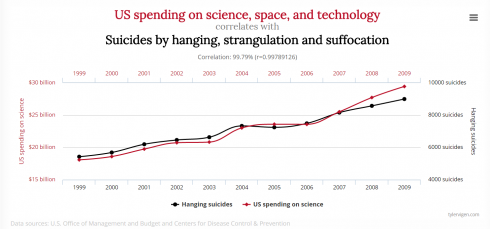
Spurious Correlations
Tyler Vigen has a great website Spurious Correlations that shows graphs of exactly that.
Great for explaining what correlation means, and why correlation does not necessarily mean causation.
How to be Lucky
The lucky try more things, and fail more often, but when they fail they shrug it off and try something else. Occasionally, things work out.
— McRaney, 2013: Survivorship Bias on You Are Not So Smart.
David McRaney synthesizes work on luck in an article on survivorship bias.
… the people who considered themselves lucky, and who then did actually demonstrate luck was on their side over the course of a decade, tended to place themselves into situations where anything could happen more often and thus exposed themselves to more random chance than did unlucky people.
Unlucky people are narrowly focused, [Wiseman] observed. They crave security and tend to be more anxious, and instead of wading into the sea of random chance open to what may come, they remain fixated on controlling the situation, on seeking a specific goal. As a result, they miss out on the thousands of opportunities that may float by. Lucky people tend to constantly change routines and seek out new experiences.
McRaney goes also points out how this survivorship bias negatively affects scientific publications (scientists tend to get successful studies published but not ones that show how things don’t work), and in war (deciding where to armor airplanes).